1. OVERVIEW

Recursion is a mechanism whereby repetition can be achieved using (at its simplest) a method that continues to call itself until some terminating value is reached, i.e. without using some specific repetition construct. The flow of control in recursion can be conceptualised as shown in the Activity Diagram given in Figure 1 (corresponding Nassi-Shneiderman chart in Figure 2). Not that, in Figure 1, the method call is a call to the same method as the calling method.

Figure 2: NS chart indicating a recursive method

The actual flow of control should therefore more accurately be described as shown in Figure 3. The Figure shows a recursive loop that iterates 4 times, i.e. the Boolean test is invoked on four occasions. The hrad (red) line marked with arrows shows the flow of control as the recursion winds up, i.e. until such a point is reached where the iterative process stops at which point the recursion is said to unwind --- the dashed (purple) line in the Figure. The light (Greyed out) processes and control flow lines show processes that are not invoked and lines that are not "exercised" in this case.

The number of recursive iterations depends on the nature of the input to the Boolean test, i.e. anything between 0 (no iterations) and an infinite (never ending) loop. Consequently the approach to indicating the flow of control in recursion as shown in Figure 3 is not a good one --- we usually do not know in advance how many recursive iterations there will be. Consequently it is more convenient to indicate recursive flow of control as shown in Figure 4. Note in the figure that we have introduced some terminology specific to recursion:

Figure 4: Recursion Activity Digarms (2)

Although Figure 4 is more succinct than Figure 3 the flow of control is not immediately obvious in all cases. It is clear that if the base case is reached immediately there is no recursive step and flow of control passes down the left hand path to the "sink". However, if the base case is reached after N iterations flow of control will initially again pass down the left hand branch but this time round to return to the recursive step. Flow of control will then loop for N iterations as the recursion unwinds (the purple line in Figure 4) until the recursion is fully unwound when flow of control will again pass on to "end".

This process is made even more confusing (at least to the novice) when the recursion includes statements to be executed before the recursive step, i.e. statement to be executed as the recursion winds up; and further statements pending to be executed as the recursion unwinds. The effect of this can best be visualised by returning to a AD of the form shown in Figure 3. This is presented in Figure 5. From this Figure we can clearly see that the statements pending will not be invoked until the recursion starts to unwind. For completeness, Figure 6 gives a NS chart depicting a recursive method with statements pending.

During the unwinding process further program statements "pending" may be called.

Note also that what has been described above is the simplest form of recursion over forms include "double recursion" (two recursive steps one pending), and "nested recursion" (one recursive step nested within another).

2. EXAMPLE PROBLEM - DECIMAL TO BINARY CONVERSION

2.1 Requirements

Develop and implement some Java software which, when given a "base 10" (decimal) natural number, will convert this number into a binary number ("base 2"). For example, given the number 41 we would expect the system to output: 00000000 00000000 00000000 00101001 The standard mechanism, for converting from decimal to binary is to repeatedly divide the decimal number by 2 and, at each division, output the remainder (0 or 1). An example is given in Figure 7 where the binary number 101001 is derived from the decimal number 41.

Figure 7: Decimal to binary conversion.

Note: A Natural number is an integer greater than or equal to zero. 2.2 Analysis A class diagram for the proposed solution is given in Figure 8. Because decimal to binary conversion is something we may want to do more often, the conversion routine has been designed as a stand alone class which must be interacted with using an application program. Note that the default constructor is used.

Figure 8: Class diagarm for decimal to binary conversion problem.

2.3 Design

2.3.1 Dec2Bin Class

Method Summary
public void	convertDec2Bin(int decimalNumber, int digitCounter)            Instance method to carry out conversion operating in a recursive manner. Method continues to recur until the given decimal number is 0, this is the base case at which point a call to the padWithZeroes method is made. As the recursion unwinds, on each iteration an appropriate digit ("0" or "1") is output.
private double	padWithZeroes(int digitCounter)            Instance method. Loops for 32-digitCounter iterations outputting a "0" on each iteration. On every eighth bit a space is output to separate the bytes making up a 32 bit integer.

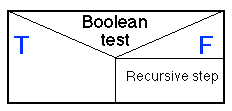
An appropriate Nassi Shneiderman design for the above is given in Figure 9. Thus in this design we have used a recursive algorithm to ensure that the binary digits are output in the correct order. If we used a simple while loop the reverse result would be produced. To avoid this we would require a temporary storage structure in which to store the digits which can then be output in reverse. The latter approach would require extra work, and consequently the recursive approach is more efficient.

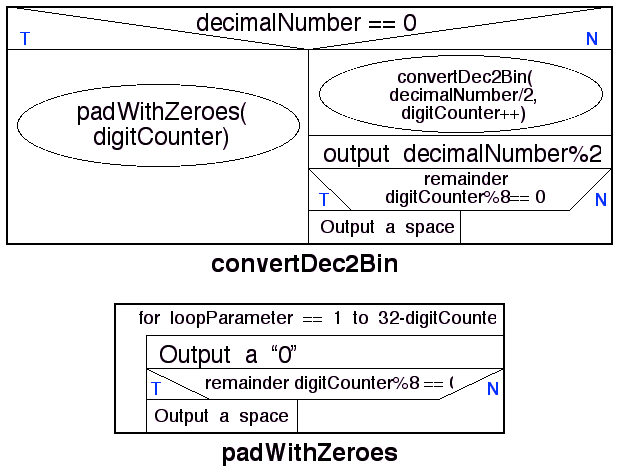
Figure 9: Nassi-Shneiderman charts for Dec2Bin class methods

2.3.2 Dec2BinApp Class

Field Summary
private static Scanner	keyboardInput            A class instance to facilitate input from the input stream.

Method Summary
public static void	main(String[] args)            Main method. Calls inputNatNum the result of which is then used to create an instance of the class Dec2Bin using the default constructor, and then calls the convertDec2Bin method in the Dec2Bin class to carry out and output the conversion.
private static int	inputNatNum()            Class method to allow a user to input a natural number. Includes error checking and recovery facility.

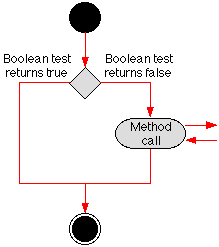
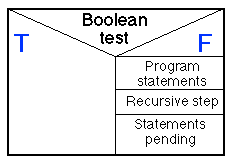
An appropriate Nassi Shneiderman design for the above is given in Figure 10, and a Activity Diagram indicating the overall flow of control through the proposed software system in Figure 11. In Figure 11 flow of control enters at the top (the riser) and loops round between the base case and the recursive step until the base case is reached. The recursion is now fully "wound up". On reaching the base case control flow continues in the bottom-left loop, and when this loop is complete the recusion starts "to unwind". The latter is indicted by the bottom-right loop.

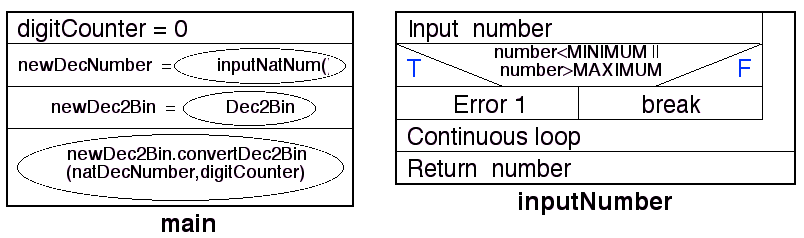
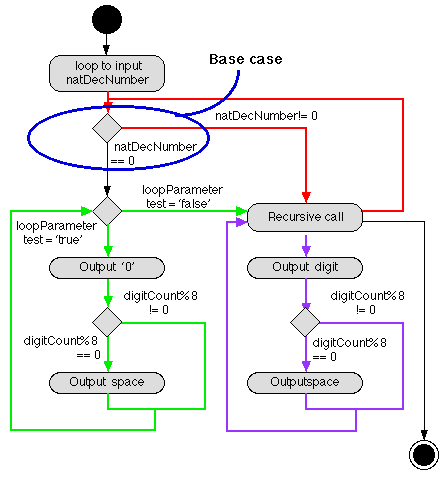
Figure 10: Nassi-Shneiderman chart for Dec2BinApp class Figure 11: Activity Diagarm for decimal to binary conversion software system.

// DECIMAL 2 BINARY
// Frans Coenen
// 30 may 1999
// Dept Computer Science, University of Liverpool

class Dec2Bin {

    // ------------------ METHODS ------------------------

    /* ------ CONVERT DECIMAL 2 BINARY */

    // Output digits and spaces between bytes when appropriate

    public void convertDec2Bin(int decimalNumber, int digitCounter) {
    
	// Base case 
	if (decimalNumber == 0) padWithZeros(digitCounter);
	 
        // Recursive step	
        else {     
            convertDec2Bin(decimalNumber/2,digitCounter+1);
            System.out.print(decimalNumber%2);
	    if (digitCounter%8 == 0) System.out.print(" ");
            }   
        }

    /* ------ PAD WITH ZEROS ------ */

    // Private class method to output a sequence of `0' characters to 
    // pad the output with, where the decimal number does not require 
    // all the 32 digits for its binary equivalent encoding. 

    private static void padWithZeros(int digitCounter) {
        final int TOTAL_DIGITS = 32;
	int loopParameter;
        int endValue = TOTAL_DIGITS-digitCounter;

        // For loop, output a `0' on each iteration
        for(loopParameter=1;loopParameter<=endValue;loopParameter++) {
            System.out.print("0");
            if (loopParameter%8 == 0) System.out.print(" ");
            }   
        }
    }

// DECIMAL 2 BINARY APPLICATION
// Frans Coenen
// 30 May 1999
// Revised: Friday 26 August 2005
// Dept Computer Science, University of Liverpool

import java.util.*;

class Dec2BinApp{

    // ------------------- FIELDS ------------------------ 
                                           
    // Create Scanner class instance
    public static Scanner keyboardInput = new Scanner(System.in);
		      
    // ------------------ METHODS ------------------------  
    
    /* Main method */
    
    public static void main(String[] args) {
        final int COUNTER=0;
	
        // Input a natural number
        int natDecNumber = inputNatNum();
	
        // Do the conversion
	Dec2Bin newDec2Bin = new Dec2Bin();
        newDec2Bin.convertDec2Bin(natDecNumber,COUNTER);
	
	// End	
	System.out.println();  
        }
	
    /* Input a natural number */
    
    private static int inputNatNum() {
        int number;
        final int MAXIMUM = Integer.MAX_VALUE;
	final int MINIMUM = 0;
	
	// Invitation to input
        System.out.println("Input an integer between " + MINIMUM + 
        		" and " + MAXIMUM + " (inclusive)");

        // Do-while loop
        do {
            number = keyboardInput.nextInt();
	    if (number < MINIMUM || number > MAXIMUM) 
	    		System.out.println("ERROR 1: Incorrect input " + 
					number + ", try again!"); 
	    else break;		
            } while (true);

        // End
        return(number);
        }
    }

$ java Dec2BinApp
Input an integer between 0 and 2147483647 (inclusive)
-1
ERROR 1: Incorrect input -1, try again!
0
00000000 00000000 00000000 00000000
[frans@frans Bin2Dec]$ java Dec2BinApp
Input an integer between 0 and 2147483647 (inclusive)
9999
00000000 00000000 0010011100001111
[frans@frans Bin2Dec]$

3. DECIMAL TO HEXADECIMAL CONVERSION

The recursive approach described above can be adapted to other types of integer conversion. For example decimal to hexadecimal conversion. The implementation for a suggested class Dec2Hex is presented in Table 4 (class digarm in Figure 12).

Figure 12: Class diagarm for Dec2Hex conversion Class.

Notes on code presented in Table 4

	The MAX_NUM_DIGITS constant is set to 3 becasuse the maximum number of digits to a 32 bit hexadecimal number is 4 (the count starts with digit 0).
	Note the use of the characters symbols 'A' through to and including 'F' to indicate the extra 6 digits available in the hexadecimal system.
	The Dec2Hex class presented here is designed to be used in conjunction with an application class very similar to the Dec2BinApp class introduced above (Table 2).

ALTERNATIVE (RECURSIVE) IMPLEMENTATION OF FIBONACCI PROBLEM