In COMP101 it was shown that the number of elements in a 1-dimensional array can be set when the application program is executed, in accordance with values specified by the user. A facility of this type is a common feature of many high-level programming languages, notable exceptions being FORTRAN and Pascal. Given our interpretation of multi-dimensional structures as 1-dimensional arrays of compound Objects, we would expect that the `bounds' of a multi-dimensional array Object can also be fixed when a program is executed. This, of course, is indeed the case. There is, however, an important feature of the Java implementation of unconstrained multi-dimensional arrays that makes these rather different from the analogous structures in languages such as, Ada, Algol68, etc.
Question: Why is the the word bounds in the paragraph above, written in inverted quotes?
Answer: Because, in Java, a k-dimensional array does not, necessarily, have exactly k `bounds' associated with it.
Suppose, for example we consider a 2-dimensional array,
| int [ ] [ ] xy; |
If we take as input some positive integer value, read into a variable, n say, then we could set specific bounds on xy by, e.g.
| xy = new int [n] [ ]; | OR |
| xy = new int [n] [n]; | OR |
| xy = new int [n-1] [n-2]; | etc |
The last two examples result in both dimensions being constrained; and the first with exactly one dimension being constrained.
If we examine the completely constrained cases more closely, we see that:
comprises n 1-dimensional arrays each having n elements.
comprises n-1 1-dimensional arrays each having n-2 elements.
What about the first case?
All we can say of
is that it defines n 1-dimensional arrays each of whose lengths is currently unconstrained.
Similarly,
defines n 2-dimensional arrays, each of which consists of n-1 rows whose exact length(s) have yet to be constrained.
and,
comprises n arbitrary and unconstrained 2-dimensional arrays.
So, what's the point?
The point is: there is no requirement, in Java, that when the n 1-dimensional arrays
do have their lengths constrained, for every single one of these to have the same length.
In other words, for a given value of n, 10 say, we could instantiate the lengths of each of the 10 1-dimensional arrays in `patterns' such as either of those in the figure below:
 | 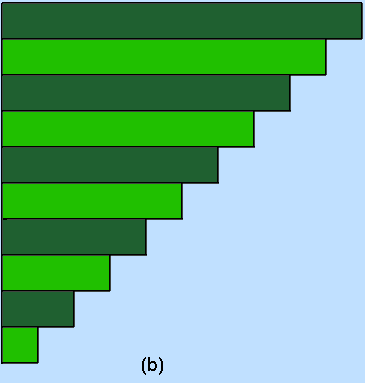 |
Figure 4.1: `2-dimensional' arrays: Possible configurations in Java.
In Figure 4.1(a), each odd numbered row contains exactly half as many elements as each even indexed row. Given an integer value, m, as the length of the even indexed arrays, we could instantiate such an allocation by
xy = new int[n][];
for (int i=0; i< n; i++)
if (i%2==0)
xy[i] = new int [m];
else
xy[i] = new int [m/2];
|
Figure 4.2: Java realisation of Array Strucure in Figure 4.1(a)
In Figure 4.1(b), the number of elements in xy[i] for i < 9 is exactly one more than the number of elements in xy[i+1], a structure that could be instantiated by
xy = new int[n][]; for (int i=0; i < n; i++) xy[i] = new int [n-i]; |
Figure 4.3: Java realisation of Array Structure in Figure 4.1(b)
Such forms are not restricted to the 2-dimensional cases. For example a 3-dimensional analogue of the organisation in Figure 4.1(b), could be realised by
xyz = new int [n][][];
for (int i=0; i < n; i++)
{
xyz[i] = new int [n-i][];
for (int j=0; j < n-i; j++)
xyz[i][j] = new int [n-i-j];
};
|
Figure 4.4: A more complex example of a `Pyramid' Structure in 3-dimensions
In this example, the n `planes' of the array xyz, are organised so that for each k < n, the 2-dimemnsional array xyz[k] is instantiated in the form of Figure 4.1(b) using the value n-k (instead of 10).
Notice, that the order in which individual dimensions are constrained is important when organising such structures: the mechanisms below although appearing to have equivalent behaviour to the implementation in Figure 4.4 will not work:
xyz = new int [n][][];
for (int i=0; i < n; i++)
{
for (int j=0; j < n-i; j++)
{
xyz[i] = new int [n-i][];
xyz[i][j] = new int [n-i-j];
};
};
|
int [][][] xyz = new int [n][][];
for (int i=0; i < n; i++)
{
for (int j=0; j < n-i; j++)
{
xyz[i][] = new int [][n-i-j];
};
xyz[i] = new int [n-i];
};
|
| Incorrect Form of Figure 4.4 (i) | Incorrect Form of Figure 4.4 (ii) |
Figure 4.5: Two Erroneous Realisations of the Structure Defined in Figure 4.4
The example in (ii), which attempts to constrain the third dimensions before the lengths of the second dimension arrays have been fixed will not even compile. The example in (i), although compiling correctly, will not result in the required form being created: the statement
will be executed n-i times (in Figure 4.4, this statement is carried out before the for loop whose counter variable is j is entered) and, as a result, only the arrays xyz[i][n-i-1] will be fully constrained (each will have length 1); the arrays of the form xyz[i][j] for any value of j other than n-i-1 will not have had space allocated and attempts to refer to elements within such will result in a run-time exception.
The examples above illustrate that a multi-dimensional array Object may be constrained to have an extremely intricate `irregular' structure, albeit one that can always be analysed in terms of the `1-dimensional array of compound Objects' abstraction that has been promoted. Such a facility is not common in other high-level languages supporting unconstrained multi-dimensional arrays, the `object-orientated' language C++ allows this, but in, for example, Ada the language syntax compels programs to constrain the bounds of all dimensions simultaneously, thus in the 2-dimensional case, each `row' of the array must contain exactly the same number of `columns'. In order to achieve a similar functionality to the Java mechanism a more complicated data structure would have to be defined.
|
Definition:
An undirected graph, G(V,E), is defined by two (finite) sets:
The edges, E(G) of an undirected graph G(V,E) are a set of (unordered) pairs of distinct vertices from V(G). The number of vertices in V(G) is called the order of G(V,E) The number of edges in E(G) is called the size of G(V,E) (Thus we may refer to a graph G(V,E) of order 10 and size 20 to describe one which has 10 vertices and 20 edges |
The Road Map Example that we presented in the second lecture can be seen as an undirected graph G(V,E) in which
|
V(G) = { A,B,C,D,E,F }
E(G) = { {A,B}, {A,C}, {A,F}, {B,D}, {C,D}, {C,E}, {C,F}, {D,F}, {E,F} }
|
|
The order of this graph is 6 The size of this graph is 9 |
The Road Map Example of Lecture 2 Interpreted as an Undirected Graph of Order 6 and Size 9
Graphs, in both the undirected form defined above, and the directed form, wherein the edges are a set of ordered pairs of distinct vertices (so that an edge (A,C) is distinct from an edge (C,A)), are an extremely important structure within most (if not all) areas of Computer Science. Although the terms by which these are referred to may differ, you will encounter graphs throughout the remainder of the degree course. Thus, within, e.g.
- Algorithmics (COMP108, COMP202, COMP301, COMP308, COMP312).
- Database Structures and Data Modelling (COMP106, COMP206, COMP302)
- Hardware systems and Computer Architecture (COMP203, COMP303)
The pervasive nature of graphs as a modelling basis within Computer Science provides some motivation for developing a simple Java packgage that can store and provide some basic operations on graph instances.
We describe the components of such for undirected graphs, as a natural application illustrating the use of unconstrained multi-dimensional arrays in Java.
3. A Basic Undirected Graph Object in Java
3.1. Requirements
Develop a package Graph that will provide the following capabilities:
- Creation and Storage of an undirected graph G(V,E) in which the order (number of vertices) is specified by the application.
- Allows the edges in a given instance to be associated with arbitrary Objects, e.g. Integer (as would be appropriate with the Road Map example where such values could represent distances) or Boolean (for which values would indicate the presence or absence of edges).
- Provides methods to:
- Set the Object value that is used to represent the absence of an edge between vertices.
- Return the value of the Object indicating the absence of edges.
- Return the number of vertices (order) in an instance.
- Return the number of edges (size) in an instance.
- Test if there is an edge present between two specified vertices in an instance of a Graph.
- Obtain the value of an Object associated with a given pair of vertices (returning the value provided in (1) (which might be the null value) if no edge exists between the two vertices).
- Change the value of an Object instance representing an edge between two specified vertices in an instance of Graph. Note that this should provide a facility that allows edges to be removed, i.e. the current non-edge Object is a legitimate parameter value.
- Convert the Graph structure into a String that when printed describes the internal structure of the Graph.
It should be noted that we have chosen to allow the datum associated with an edge to be an Object of arbitrary type, so ensuring that a plethora of different constructors and methods does not have to be written, i.e. one for each type required.
Closer inspection of the structures described, suggests the Class Diagram indicated in Figure 4.6 below,
Figure 4.6: Class Diagram for Graph Class
Whilst a 2-dimensional array is a `natural' representation for graphs, if we look at the
form suggested to implement the Road Map example, in Lecture
2, we see that it has one rather obvious weakness: it uses (more than) twice
as many elements than are necessary to record all of the information pertinent to the graph structure, i.e.
contains exactly the same value as the element
This is not something particular to the example used but is a behaviour
that will arise in any undirected graph form, i.e. the graph structures
that are typically used do not have edges joining a vertex to itself; since the graph is undirected
there is no distinction between describing an edge in the form {v,w} and the form {w,v}.
Thus a less wasteful structure for storing undirected graph structures would be one
in which:
Desiderata for `efficient' Undirected Graph Storage.
Of course the second of these requirements ought to be dealt with (within the Class definition itself)
in a consistent fashion. There is, however, no need for applications that
might use the Graph class to be aware of what this is. Indeed, in
keeping with the principle of data hiding, making the mechanism used visible to users
(or, worse, requiring that applications were required to supply references to edges
in a `consistent' manner) would be poor design style.
Fortunately, there is a simple approach that the Class methods accessing the graph
representation can use to identify a reference to an edge {v,w} as equivalent to a reference
supplied in the form {w,v}: since (a) obviates the need to deal with storing `edges' {v,v},
and that the access to edge information will be via an array element - g[v][w] - hence,
with integer indices, it can be arranged (internally within the Class definition) that
accesses are predicated on the assumption v < w.
We can now examine the realisation of the Graph class in more detail.
Graph Class Fields
The fields
private int size
private Object NonEdge=null
in the Graph Class Diagram
will record the number of vertices, number of edges, and the value that indicates the absence
of an edge between two vertices. The last of these being instantiated to to a default setting
of the null Object.
The core of the undirected graph representation in which all of the edge data for the
instance will be maintained is the 2-dimensional array of Objects
In keeping with the requirement that undirected graphs of arbitrary order may be
instantiated, this is in an unconstrained format.
In order to appreciate exactly how an undirected n-vertex graph is held within
this array, we turn to the implementation of
The Constructor Graph(int n)
The integer parameter, n, defines the number of vertices in the graph instance.
In modelling an undirected n-vertex graph using the 2-dimensional array matrix [][]
the total number of cells used will be exactly (n*(n-1))/2.
How do these correspond to the possible edges in an n-vertex undirected graph?
Suppose, we look at the specific case of n=8. Here we have to provide for
the edges:
So we have a row for each vertex (except the highest indexed vertex) and within the
row for vertex number k, a cell for each vertex whose index is strictly larger
than k, i.e. the k'th row contains exactly n-k columns - one for each
vertex except those whose index is less than or equal to k. Hence,
Figure 4.7: The Constructor Graph(int n)
Now, suppose that we wish to access the element of this array that corresponds to an
edge between two distinct vertices v and w, where, assuming the convention mentioned
above, we have
Given the, rather irritating, feature of Java that the first element of a length k array
is indexed by 0 and its last by k-1, we cannot simply inspect the element
Certainly the data relevant to a vertex with index v is all contained within
the 1-dimensional array of Objects
within this array,
From which we see that the edge {v,w} can be accessed in the element
It is worth stressing, again, that this translation from a pair of distinct vertex
labels - v and w - into a specific element of a 2-dimensional array, i.e.
matrix [v-1][w-v-1] ought to be hidden from (and inaccessible to)
applications using the Graph class: such applications
will only want to recover information concerning an edge by supplying two distinct
vertex labels.
We can now address the realisation of the Class methods. We note from
the Class Diagram that these are all Instance Methods
Graph Class Methods
The methods
just provide access to the values of these data fields in an Instance, and so are realised
by,
Figure 4.8: Methods to obtain the order and size of an Instance
The method
that
is used to supply the current setting of the value used to indicate the absence of an
edge between two vertices (held in the field NonEdge),
is a little bit more involved: its setting might be to
the null reference, and an error might result if this were used in
the invoking application.
It is, therefore, necessary to check if this is the case and, should it be so, to return the literal
String "null".
Figure 4.9: Obtaing the current `Non-edge' setting
The method
is used to test whether the Graph instance contains an edge joining
vertices v and w. When this is invoked the parameters will be values
between 1 and order (and should be distinct). As has been stressed earlier, the realisation
of the class is responsible for relating these values to the correct cell of the
2-dimensional array, using the approach descirbed earlier.
Figure 4.10: Boolean test for presence (true)/absence (false) of an edge {v,w}
In order to permit applications to choose a different value to represent the
absence of an edge the method
is used. Again care has be taken should an application wish to restore the default
null setting by supplying this as a literal
String. In addition, the array elements that held the
former NonEdge value have to updated to hold the new value set.
Figure 4.11: Changing the non-edge indicator
The methods described so far have largely been concerned with customising various class
fields to application-specific setting. The next two methods are likely to be the two
most heavily employed within any application employing the Graph class
The former sets the value of the edge {v,w} to the Object edge_val.
The latter returns the current Object associated with the
edge {v,w}.
Since the current non-edge indicator is a valid setting of edge_val the SetEdge method
provides a mechanism for deleting an edge from the Graph instance. This method
must also ensure that the size field (recording the number of edges in the instance)
is correctly maintained after this method has completed.
Figure 4.12: Setting and Obtaining the current status of an edge {v,w}
Finally, we have the method
that will translate the current graph form into a String suitable
for printing.
Figure 4.13: Creating a suitable printing form of a Graph Instance.
The complete Graph Class Implementation is given below
Figure 4.14 The Undirected Graph Class
The Java program presented below provides a simple example of the Graph
class in practice.
This reads in the integer value, n, defining the number of vertices
and uses Integer as the basic edge Object,
(recall that the primitive types are not recognised as Objects in Java, so
we must use the Wrapper class Integer
to store these). The Integer 0 is used as the non-edge Object, and we use the
Integer 1 to indicate the presence of an edge between two vertices.
All that the program below does is to read in a sequence of (n*(n-1)/2) integer values
(recall that this is the number of possible edges in an n-vertex undirected graph), interpreting
positive values as indicating edges and other values as indicating no edge.
The program then computes the graph complement - the graph that
results by adding edges which are missing and removing edges which were present.
Figure 4.15 A Simple Application of the Graph Class
If we run this program using the input,
this will produce the output

3.2. Analysis
a)
No elements are used to record information concerning `edges' of the form {v,v} b) Exactly one of the edges {v,w} and {w,v} has information concerning it stored in the structure
{1,2} {1,3} {1,4} {1,5} {1,6} {1,7} {1,8} {2,3} {2,4} {2,5} {2,6} {2,7} {2,8} {3,4} {3,5} {3,6} {3,7} {3,8} {4,5} {4,6} {4,7} {4,8} {5,6} {5,7} {5,8} {6,7} {6,8} {7,8}
public Graph(int n)
{
order = n; size=0;
matrix = new Object[n-1][]; // the number of `rows' for n vertices
//
for (int i=0; i < n-1; i++)
matrix[i] = new Object[n-i-1]; // the number of `columns' for each row.
//
for (int i=0; i < n-1; i++)
for (int j=0; j < n-i-1; j++)
matrix[i][j] = NonEdge; // assumes no edges are present.
}
public int OrderOf()
{
return order;
};
//
public int SizeOf()
{
return size;
}
public Object NoEdge()
{
if (!(NonEdge==null)) // We have to test this, in order to
return NonEdge; // avoid a NullPointerException error
else // which would occur in this
return "null"; // particular case.
}
public boolean IsEdge( int v, int w)
{
if (v < w)
return !(matrix[v-1][w-v-1]==NonEdge); // Data concerning vertex v
// w.r.t `higher' numbered
// vertices is in row `v-1'
else
return !(matrix[w-1][v-w-1]==NonEdge);
}
public void SetNonEdgeValue ( Object no_edge )
{
if ( (no_edge.toString()).equalsIgnoreCase("null") ) // Can't pass null
{ // reference directly and
for (int i=1; i < order; i++) // so we use the String encoding
for (int j=i+1; j < order+1; j++) // to indicate this setting.
if (!IsEdge(i,j))
matrix[i-1][j-i-1] = null;
NonEdge=null; // Do AFTER updating matrix[][]!
}
else
{
for (int i=1; i < order; i++) // Same procedure but where a
for (int j=i+1; j < order+1; j++) // non-null setting is being used.
if (!IsEdge(i,j))
matrix[i-1][j-i-1] = no_edge;
NonEdge = no_edge;
};
}
public void SetEdge ( Object edge_val, int v, int w)
{
if (v==w)
matrix[v-1][w-v-1] = null; // This is a bit clumsy. Will force an
// ArrayOutofBoundsException,
// which is what's needed.
else if (v < w)
{
if (!IsEdge(v,w)) // If there's no edge {v,w}
{
if ( !(edge_val.equals(NonEdge)) ) // and we're about to add it then
{
size = size+1; // the number of edges increases by 1.
};
}
else // If there IS an edge {v,w}
{
if ( edge_val.equals(NonEdge) ) // and we're about to remove it then
{
size=size-1; // the number of edges decreases by 1.
};
};
matrix[v-1][w-v-1] = new Object(); // Probably not needed (a precaution).
matrix[v-1][w-v-1] = edge_val; // Store the new value.
}
else
this.SetEdge(edge_val,w,v); // Can't expect applications to ensure
// {v,w} are supplied with v < w so arrange
// this properly.
// Note that if v=w is NOT caught then
// this Method will recurse indefinitely.
// (Don't have to worry about this
// in IsEdge(v,w)
// because an Array bound exception
// will be raised
// by the run-time system if v=w).
}
//******************************************************************//
// Obtain the value of the Object associated with edge {v,w} //
//******************************************************************//
public Object GetEdge (int v, int w)
{
if (v==w)
return matrix[v-1][w-v-1]; // See similar remarks re. SetEdge
else if (v < w)
if (IsEdge(v,w)) // if there's a `real' edge then
return matrix[v-1][w-v-1]; // just return the associated Object.
else // If there's not a `real' edge
if (NonEdge==null) // have to make sure a NullPointerException
// isn't generated.
return "null";
else
return NonEdge.toString(); // Returns the current NonEdge object value.
else
return this.GetEdge(w,v);
}
//*********************************************************************//
// Convert the Graph structure to a String form that is suitable for //
// output. The edges {v,w} are stored in a String in which newline //
// characters separate the different vertex details. //
// The printing form is as order-1 distinct lines, the k'th line //
// containing exactly one fewer item than the (k-1)'st line. Hence //
// //
// Line 1: Status of edges {1,2} {1,3} {1,4} ... {1,order} //
// 2: {2,3} {2,4} {2,5} ... {2,order} //
// ... //
// k: {k,k+1} {k,k+2} ... {k,order} //
// ... //
// order-1 {order-1,order} //
//*********************************************************************//
public String toString()
{
String res=new String();
for (int i=1; i < order; i++)
{
for (int j=i+1; j < order+1; j++)
{
res = res+GetEdge(i,j).toString()+" ";
};
res = res+"\n";
};
return res;
}
//
// COMP102
// Example 6: Undirected Graph Class
//
// Paul E. Dunne 25/10/99
//
public class Graph
{
//
// Fields
//
private Object [][] matrix; // This will record the definition
// of the Graph structure.
//
// N.B. Declaration as 2-D array of Object
// so that the graph edges may be associated
// with both primitive types (via Wrappers) and
// Compound types. Typical instantiations might
// be as Boolean (matrix[v][w] is TRUE if and
// only if there is an edge between vertex v and
// vertex w); Integer (so that the values stored
// represent the `distance' separating two
// vertices); String (so that edges are
// associated with `text')
//
private int order; // The number of vertices in this Graph Instance.
private int size; // The number of edges in this Graph Instance.
// This value is dynamically updated when
// the effect of relevant Instance methods
// results in a change in the size of the Graph.
//
private Object NonEdge = null; // It is useful to have a distinctive value that
// can indicate if no edge is present between
// {v,w} in the Graph. Here we give a default
// setting to the null Object. In specific
// instantiations, however, this could be set
// appropriately depending on the application
// used, e.g. as the Boolean FALSE if using the
// basic Boolean representation above; as the
// largest (smallest) possible Integer where
// edges are associated with `distances'; as the
// empty String ("") in a labelling context, etc.
//*****************************************************//
// Constructor Definition //
//*****************************************************//
// The single Constructor provided, allocates storage //
// for an n-vertex Graph. //
// The 2-dimensional array matrix[][] is configured //
// so that it comprises n-1 rows, the k'th row (k < n) //
// containing exactly one fewer column than the //
// (k-1)'st //
//*****************************************************//
// Access and modification to this array can ONLY BE //
// performed via the Instance methods defined below //
// cf. Presence of private modifier in the field //
// definition of matrix[][] //
//*****************************************************//
public Graph(int n)
{
order = n; size=0;
matrix = new Object[n-1][]; // the number of `rows' for n vertices
//
for (int i=0; i < n-1; i++)
matrix[i] = new Object[n-i-1]; // the number of `columns' for each row.
//
for (int i=0; i < n-1; i++)
for (int j=0; j < n-i-1; j++)
matrix[i][j] = NonEdge; // assumes no edges are present.
}
//*********************************************************************//
// Instance Methods //
//*********************************************************************//
// The following methods provide access to the settings of `simple' //
// Class fields. //
//*********************************************************************//
// public int OrderOf() : Provides access to value of the order field //
// i.e. the number of vertices in this Graph. //
//*********************************************************************//
// public int SizeOf() : Access to the field holding the number of //
// edges in this Graph. //
//*********************************************************************//
// public Object NoEdge(): Access the current setting of the Non-edge //
// Object value. //
//*********************************************************************//
public int OrderOf()
{
return order;
};
//
public int SizeOf()
{
return size;
}
//
public Object NoEdge()
{
if (!(NonEdge==null)) // We have to test this, in order to
return NonEdge; // avoid a NullPointerException error
else // which would occur in this
return "null"; // particular case.
}
//*********************************************************************//
// Given two (distinct) vertices (v and w) with 1 <= v,w <= order, //
// return true if this graph contains an edge connecting them. //
//*********************************************************************//
// N.B. Applications using the Graph Class do not have to be aware of //
// the storage as a 2-dimensional array. In this, and other methods, //
// the values v and w are transalated to give the correct `cell' of //
// the 2-dimensional array structure indicating the current state of //
// the `edge' {v,w}. //
//*********************************************************************//
public boolean IsEdge( int v, int w)
{
if (v < w)
return !(matrix[v-1][w-v-1]==NonEdge); // Data concerning vertex v
// w.r.t `higher' numbered
// vertices is in row `v-1'
else
return !(matrix[w-1][v-w-1]==NonEdge);
}
//*********************************************************************//
// Change the setting of the Object used to indicate that an edge is //
// NOT present between two vertices updating the Graph representation //
// so that the new Object value is stored. //
//*********************************************************************//
public void SetNonEdgeValue ( Object no_edge )
{
if ( (no_edge.toString()).equalsIgnoreCase("null") ) // Can't pass null
{ // reference directly and
for (int i=1; i < order; i++) // so we use the String encoding
for (int j=i+1; j < order+1; j++) // to indicate this setting.
if (!IsEdge(i,j))
matrix[i-1][j-i-1] = null;
NonEdge=null; // Do AFTER updating matrix[][]!
}
else
{
for (int i=1; i < order; i++) // Same procedure but where a
for (int j=i+1; j < order+1; j++) // non-null setting is being used.
if (!IsEdge(i,j))
matrix[i-1][j-i-1] = no_edge;
NonEdge = no_edge;
};
}
//*********************************************************************//
// The main Instance method for defining a particular graph structure. //
//*********************************************************************//
// This allows edges to be added to the Graph and to be removed: //
// To add an edge {v,w} supply an edge setting that is different from //
// the current NonEdge setting. //
// To remove an edge {v,w} invoke the method with edge_val instantiated//
// to the current NonEdge Object value. //
//*********************************************************************//
public void SetEdge ( Object edge_val, int v, int w)
{
if (v==w)
matrix[v-1][w-v-1] = null; // This is a bit clumsy. Will force an
// ArrayOutofBoundsException,
// which is what's needed.
else if (v < w)
{
if (!IsEdge(v,w)) // If there's no edge {v,w}
{
if ( !(edge_val.equals(NonEdge)) ) // and we're about to add it then
{
size = size+1; // the number of edges increases by 1.
};
}
else // If there IS an edge {v,w}
{
if ( edge_val.equals(NonEdge) ) // and we're about to remove it then
{
size=size-1; // the number of edges decreases by 1.
};
};
matrix[v-1][w-v-1] = new Object(); // Probably not needed (a precaution).
matrix[v-1][w-v-1] = edge_val; // Store the new value.
}
else
this.SetEdge(edge_val,w,v); // Can't expect applications to ensure
// {v,w} are supplied with v < w so arrange
// this properly.
// Note that if v=w is NOT caught then
// this Method will recurse indefinitely.
// (Don't have to worry about this
// in IsEdge(v,w)
// because an Array bound exception
// will be raised
// by the run-time system if v=w).
}
//******************************************************************//
// Obtain the value of the Object associated with edge {v,w} //
//******************************************************************//
public Object GetEdge (int v, int w)
{
if (v==w)
return matrix[v-1][w-v-1]; // See similar remarks re. SetEdge
else if (v < w)
if (IsEdge(v,w)) // if there's a `real' edge then
return matrix[v-1][w-v-1]; // just return the associated Object.
else // If there's not a `real' edge
if (NonEdge==null) // have to make sure a NullPointerException
// isn't generated.
return "null";
else
return NonEdge.toString(); // Returns the current NonEdge object value.
else
return this.GetEdge(w,v);
}
//*********************************************************************//
// Convert the Graph structure to a String form that is suitable for //
// output. The edges {v,w} are stored in a String in which newline //
// characters separate the different vertex details. //
// The printing form is as order-1 distinct lines, the k'th line //
// containing exactly one fewer item than the (k-1)'st line. Hence //
// //
// Line 1: Status of edges {1,2} {1,3} {1,4} ... {1,order} //
// 2: {2,3} {2,4} {2,5} ... {2,order} //
// ... //
// k: {k,k+1} {k,k+2} ... {k,order} //
// ... //
// order-1 {order-1,order} //
//*********************************************************************//
public String toString()
{
String res=new String();
for (int i=1; i < order; i++)
{
for (int j=i+1; j < order+1; j++)
{
res = res+GetEdge(i,j).toString()+" ";
};
res = res+"\n";
};
return res;
}
}
4. A Simple Illustration of the Graph Class in Use
//
// COMP102
// Example 7: Simple Application of the Graph Class
//
// Paul E. Dunne 28/10/99
//
import java.io.*;
import Graph; // The Graph Class Definition.
import PED_NumberIO; // Ignore this (it's my own solution to
// to an irritating I/O problem.
public class SimpleGraphApp
{
public static InputStreamReader input = new InputStreamReader(System.in);
public static BufferedReader keyboardInput = new BufferedReader(input);
static Graph G;
static final Integer Present = new Integer(1); // Object to indcate an edge
static final Integer Absent = new Integer(0); // Object to indicate no edge.
// N.B. Use of wrapper.
static int n; // Will contain the number
// of vertices (G's order)
static int edge;
//
public static void main(String[] args) throws IOException
{
System.out.println("Number of vertices in the Graph?:");
n= new Integer(keyboardInput.readLine()).intValue();
G = new Graph(n); // Set up the n-vertex Graph
G.SetNonEdgeValue(Absent); // and the non-edge indicator
// to be used.
for (int v=1; v < G.OrderOf(); v++)
for (int w=v+1; w < G.OrderOf()+1; w++)
{
edge =PED_NumberIO.get_int(keyboardInput);
if (edge > 0)
G.SetEdge(Present,v,w);
else
G.SetEdge(Absent,v,w);
};
System.out.println(G.toString());
//
// Now compute the Complement of G
//
for (int v=1; v < G.OrderOf(); v++)
for (int w=v+1; w < G.OrderOf()+1; w++)
if (G.IsEdge(v,w))
G.SetEdge(Absent,v,w);
else
G.SetEdge(Present,v,w);
System.out.println(G.toString());
}
}
10 2 3 4 5 6 0 8 0 0 0 4 0 6 0 8 0 10 4 0 0 0 8 9 0 0 0 7 0 0 10 6 0 8 0 0 0 8 9 0 8 0 10 9 10 10
1 1 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 0 0 1 1 1 0 0 1 1 1 0 1 1 0 0 1 0 1 1 1 0 0 1 0 1 0 0 0 0 5. Summary
(Notes prepared and maintained by Paul E. Dunne, October 1999)