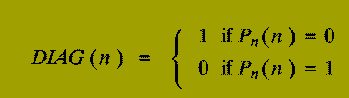Computability and Complexity
Comparing Algorithms
Computability and Complexity
The final part of the course deals with the issue of
assessing how difficult
specific computational problems are to solve.
Given a description of a particular problem a number of questions arise:
-
Is it possible to design an algorithm which solves the problem?
-
Is it possible to design an efficient algorithm which solves the problem?
-
How can one tell if a given algorithm is the `best possible'?
These questions are imprecisely formulated:
-
What exactly is meant by the term `problem'?
-
What distinguishes algorithms which can be implemented
from those which cannot?
-
What is meant by terms such as:
-
Difficulty
-
Efficient
-
Best
COMPUTABILITY THEORY
and
COMPUTATIONAL COMPLEXITY THEORY
are the fields of Computer Science concerned with the
questions raised earlier.
Computability Theory
is concerned with identifying one particular class of
INTRACTABLE PROBLEMS
(Those for which no `effective' algorithm exists)
One aim of
Computational Complexity Theory
is to identify solvable problems that are intractable in the sense that
No Efficient Algorithm Exists
which solves them.
Both areas require a formal definition of the concepts:
Problem
Algorithm
Complexity Theory also proposes definitions for the ideas of
Problem Difficulty
Algorithm Efficiency
Best Algorithm
Computational Problems
At the lowest level of abstraction any computer program may be viewed as
a means of producing
Specific Output Values
from
Given Input Data
i.e. Programs compute functions whose domain is the set of valid inputs
and whose range is the set of possible outputs.
In practice the input and output are (ultimately) represented in binary
Hence any program may be viewed as (computing) some function
f : {0,1}^* -> {0,1}^*
({0,1}^* is the set of all finite strings
(or words) containing only 0s and 1s.
It is only necessary to consider such functions as have
range {0,1}. These are known as
Decision Problems
Summary
-
All computer programs may be viewed as computing functions
-
Since all computers employ binary notation, such functions
are defined over sets of binary strings.
-
In considering the question `what problems can be solved
by computers' it is sufficient to concentrate on decision problems
Hence the question
What problems can be solved by computers?
is equivalent to
What decision problems can be solved?
Decision Problems
Any binary string can be viewed as the representation
of some natural number. Thus for decision
problems on binary strings we can concentrate on the
set of functions of the form
f : N -> {0,1}
That is `problems' of the form
Input: n a natural number
Output: 1 if n satisfies some property; 0 if n does not satisfy it.
Examples:
-
EVEN: Returns 1 if n is an even number; 0 if n is an
odd number
-
PRIME: Returns 1 if n is a prime number; 0 if n is a
composite number.
-
ADA_PROGRAM: Returns 1 if n written in
binary corresponds to the ASCII representation of
a syntactically correct ADA program; 0 otherwise.
Notice that the last example shows that we are not restricting attention to merely `arithmetic'
decision problems.
What is a `reasonable' algorithm?
In all programming systems
-
Programs have a finite number of instructions.
-
Progams make use of instructions and operations from a
finite set of basic operations
-
Programs should come to a halt for any valid input data.
An effective algorithm is one which meets these criteria.
Suppose we can show that an ADA program cannot be written which solves some problem.
Why should one take this as evidence that
NO PROGRAM (ALGORITHM) AT ALL
exists for the problem?
In other words
How can it be argued that results on computability apply to all types of
computer?
(Past, Present, and Future)
The answer is that such results are proved with
respect to abstract models of computation
that capture all the essential elements of a typical computer.
A `typical computer' has
-
Memory
-
Input and Output Mechanisms
-
A processor handling a finite instruction set.
In an abstract model we can permit an infinite supply of memory. The only
restraint on an algorithm is that it can only
use a finite amount of memory when dealing
with any single input (which, if the algorithm terminates, is all that could be
accessed).
This is not an unrealistic assumption: we do not want to
classify a problem as
unsolvable just because on some real machines there
may not be enough memory available.
The first abstract model of computation was defined by Alan Turing in 1936. This had:
-
An infinite memory of single bit cells.
-
Its `processor' dealt with only two types of `instruction'
-
A stop instruction which would return a result (0 or 1).
-
A test instruction which would read and write to a single bit of memory,
examine an adjacent memory location, and jump to another instruction.
Although the instruction set of the Turing Machine is extremely limited
Turing machine programs can be written to solve any decision problem that
can
be solved on a `normal' computer.
The Church-Turing Hypothesis
-
The class of decision problems that can be solved by any reasonable model of
computation
is exactly the same as the class of decision problems that can be solved
by Turing machine
programs.
Since 1936 several thousand different models of computation have been proposed,
e.g.
-
Post Systems
-
Markov Algorithms
-
lambda-calculus
-
Gö del-Herbrand-Kleene Equational Calculus
-
Horn Clause Logic
-
Unlimited Register Machines
-
ADA programs on unlimited memory machines
Every single one of these satisfies the Church-Turing hypothesis, i.e. anything
that can
be solved by a Turing machine program can be programmed in
any one of the system above and
vice-versa
The importance of the Church-Turing hypothesis is that it allows us, without any
loss of generality, to consider computability results solely with respect to
ADA programs on unlimited memory computers
Suppose P is some decision problem.
The Church-Turing hypothesis asserts
There is no Turing machine program that computes P
IF AND ONLY IF
There is no ADA program which solves P
Because we can (in principle) write a Turing machine program which
can exactly simulate the behaviour of any given ADA program.
Similarly, we can write an ADA program which can exactly simulate the
behaviour of any given Turing machine program.
The discussion above has, casually, assumed that there are decision
problems for which algorithms do not exist.
Why should we believe that there are actually any such problems?
(nothing above has given any evidence for the assumption made).
We can prove that there exist decision problems for which no
algorithm exists by employing a method of argument called
Diagonalisation
This can used to show that there are `more' different decision problems
than there are different ADA programs.
If there are `more' decision problems than programs then it must be the
case that some decision problems cannot be solved by programs since
since a single program can solve only a single decision problem.
Suppose we are given two sets of items, A and B, say, e.g.
A = Set of all students registered for the course 2CS46
B = Set of all students registered for the course 2CS42
How can we tell if there are more items in A than there are in B?
By `counting' the number of items in each set.
-
How many different decision problems are there?
A decision problem, f, is specified by saying for
each number n what the
value of f(n) is. f(n) can
either be 0 or 1. So we have:

Thus there are an infinite number of distinct decision problems.
How many different ADA programs are there which take a single number, n,
as input
and return a 0 or 1 as their result?
Infinitely many. Since there are clearly infinitely
many such programs which contain a loop of the form
for i in 1..m loop
s := 0;
end loop;
`Counting' is all right when the sets being compared are finite.
`Counting' does not appear to tell us anything
when both sets are infinite.
Q: What do we actually do when we `count' the number of items in a set?
A: To each item we attach a unique `label': 1,2,3,4,...
Thus, in comparing the sizes of two finite
sets, A and B, we attach `labels'
to the items in A, and `labels' to the items in B and we say that
A is larger than B
if we use more `labels' (i.e. numbers) with A than we do with B
.
But why use `numbers' as the `labels' to count with?
We could use items in A to label items in B (i.e. count) and, if
A is larger than B, then at least one item in A will not
have been used to label any item in B.

And we can `count' B by using the `labels'
ALF for AVA
BABS for BOB
CALUM for CAROL
DORA for DAVE
ED for ELLA
FIONA for FRANK
and now GARY has not been used to label any element of B and so we
can say that
A is larger than B'
What if both A and B are infinite sets?
If it can be shown that for every way of labelling items in B with
items in A
there is at least one item of A
which is not used as a label then, again,
we can state that:
A is larger than B'
Diagonalisation
is a method of argument that allows this to be shown.
Let:
A = The set of all decision problems,
f : N -> {0,1}.
B = The set of all ADA programs.
We can enumerate (i.e. list) every single ADA
program. That is there is an algorithm
which will output every single different ADA program in turn, e.g.
i := 1;
loop
if ADA_PROGRAM ( i ) = 1 then
put ( Binary representation of i );
end if;
i :=i + 1;
end loop;
(Recall that ADA_PROGRAM ( n ) is the decision problem which tests if n
written in binary corresponds to the ASCII character representation of a compiling
ADA program)
Thus we can talk about a
`First' ADA program, P1
`Second' ADA program, P2
`Third' ADA program, P3
...
`n''th ADA program, Pn
...
i.e. the 1st, 2nd, 3rd, ..., nth, ..., program that is output by
the procedure above.
And so we can form an infinite table, T:
| | 1 | 2 | 3 | .. | n | .. |
| P1 | *P1 (1) | P1 (2) | P1(3) | .. | P1(n) | .. |
| P2 | P2 (1) | *P2 (2) | P2 (3) | .. | P2 (n) | .. |
| P3 | P3 (1) | P3 (2) | *P3 (3) | .. | P3 (n) | .. |
| .. | | .. | | .. | .. | .. |
| .. | | .. | | .. | .. | .. |
| Pn | Pn (1) | Pn (2) | Pn (3) | .. | *Pn (n) | .. |
| .. | | .. | | .. | .. | .. |
| .. | | .. | | .. | .. | .. |
If it is the case that every decision problem, f, is computed
by at least one ADA program, then in the table above which `labels'
each ADA program with a decision problem:
For every decision problem f
There is an ADA program, Pf,
which is labelled with f.
i.e. There is a row, Pf, of the table such
that Pf( n ) = f( n ) for all n.
What about the following decision problem?
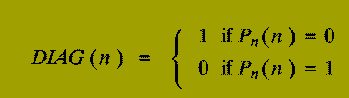
DIAG is well-defined, since our table, T, above exists.
BUT
DIAG cannot be the decision problem
that is labelling
P1 (DIAG(1) /= P1(1))
OR that labelling P2 (DIAG(2) /= P2(2))
OR that labelling P3 (DIAG(3) /= P3(3))
...
OR that labelling Pn (DIAG(n) /= Pn(n)).
And so, the decision problem, DIAG, does not
label any Pn, in the table T.
Now matter how the ADA programs are ordered, we can always define a decision problem,
DIAG, as above, which does not label any program in the ordering.
In consequence:
There exist decision problems
which cannot be solved by
ANY
ADA-program
There exist decision problems
for which
NO ALGORITHM AT ALL EXISTS
Decision problems for which no algorithm exists are called:
Undecidable
Diagonalisation indicates that undecidable decision problems
exist
It does not help in finding an
explicitly defined
undecidable decision problem.
That is:
It does not identify an undecidable decision problem whose input and output
behaviour can be given with a finite description.
The decision problems
are explicitly defined (we can give a finite description of each problem; we
do not have to state each individual output for each individual input: that
would be an infinite length description)
But, all three of these are obviously,
decidable
i.e. an algorithm (ADA program) can be written to solve them.
Alan Turing in 1936 exhibited the first explicit example of an undecidable decision
problem:
The Halting Problem
The Halting Problem, HP, is the following decision problem:
Input: An ADA program, P, (which takes as input a single number, n) and
an input w for P.
Output: 1 if P comes to a halt when run with input w
; 0 if P never
halts when started with input w.
It may be objected that HP is not a decision problem in the sense that we
have been using to date since:
-
It has 2 items of input instead of one.
-
One of its inputs is a `program' not a number.
However we can define an equivalent decision problem HP2 to which
such objections do not apply.
HP2 takes as input a single number, m. This number is a valid input if
-
m has a binary representation of the form
x 00000000 y
where x and y are binary strings;
-
x is the ASCII binary representation of an
ADA program, Px say,
which takes a single number as input and returns a zero or one as output.
Clearly
-
The problem of checking whether an input is valid is decidable.
-
No algorithm exists for HP if and only if no algorithm exists for HP2 (since we
can translate from inputs for HP to inputs for HP2 and vice-versa).
(Note: the `encoding trick' described above can be applied to transform any decision
problem with `multiple inputs' into an equivalent one with a single number as input).
Given this fact we will deal with the more `natural' problem HP instead of the
precisely encoded version HP2.
THEOREM
The Halting Problem (HP) is undecidable
Thus there is no algorithm which solves the Halting Problem.
PROOF
Suppose that there is an ADA program, HALT, which solves the Halting Problem, HP.
That is:
There is an ADA program, HALT, which
-
Reads an ADA program, P, and a single number, w, as its input.
-
If P halts when given w as input then HALT returns 1
as output.
-
If P does not halt when given w as input then HALT returns
0 as output.
Since HALT is assumed to exist we can write an ADA program, BAD say, which uses
HALT as a sub-procedure.
procedure BAD is
Q : integer;
function HALT (P integer;
w integer)
return boolean is
if ADA_PROGRAM(P) then
--**********************************
-- Halting problem program goes
-- here.
--*********************************
end if;
end HALT;
begin
get (Q);
if HALT (Q,Q) then
loop
put ("NOT OK");
end loop;
else
put ("OK");
end if;
end BAD;
What does BAD do?
-
BAD reads a single number, Q, as input.
-
If Q, written in binary, corresponds to an ADA program which
takes a single number as input then:
-
BAD tests whether the program represented by Q halts when given th
e
number Q as input (using the Halting Problem procedure, HALT, to
perform the test).
-
If the Halting problem procedure says that Q halts when started with
input Q then BAD goes into a non-terminating loop.
-
If the Halting problem procedure says that Q fails to halt when started with
input Q then BAD prints a message and stops.
-
HP (which HALT solves) takes an ADA program and single number as input.
-
The input for BAD should be a number which (when written in binary) is an
ADA program which takes a single number as input.
-
BAD is an ADA program (since HALT is an ADA program).
THEREFORE
There is a number,
BAD_NUMBER,
which when written in binary
corresponds exactly to the
ASCII representation of the
ADA program BAD
BAD_NUMBER is therefore a valid input for the ADA program BAD.
What happens if BAD is given
BAD_NUMBER
as input?
EITHER
BAD halts on input
BAD_NUMBER
OR
BAD does NOT halt on input
BAD_NUMBER
Suppose
BAD halts on input BAD_NUMBER.
This can only happen if
HALT( BAD_NUMBER, BAD_NUMBER )
is false,
But what does this mean? It means that
The program corresponding to BAD_NUMBER does not halt on input
BAD_NUMBER.
But `the program corresponding to BAD_NUMBER' is BAD
i.e.
HALT( BAD_NUMBER, BAD_NUMBER )
is false,
means that
BAD does NOT halt on input
BAD_NUMBER
On the other hand, suppose
BAD does NOT halt on input
BAD_NUMBER.
This can only happen if
HALT( BAD_NUMBER, BAD_NUMBER )
is true,
But what does this mean? It means that
The program corresponding to BAD_NUMBER halts on input
BAD_NUMBER.
But `the program corresponding to BAD_NUMBER' is BAD
i.e.
HALT( BAD_NUMBER, BAD_NUMBER )
is true,
means that
BAD DOES halt on input BAD_NUMBER
In summary we have shown that:
-
If a program to solve the Halting problem, HP, exists then the program, BAD exists.
-
BAD on any valid input either halts or does not halt.
-
BAD_NUMBER is a valid input for BAD.
-
BAD on input BAD_NUMBER fails to halt only if BAD on
input BAD_NUMBER halts.
-
BAD on input BAD_NUMBER halts only if BAD on input BAD_NUMBER
fails to halt.
We can therefore conclude that
No program to solve the
Halting Problem, HP,
can be written
i.e.
The Halting Problem
is
undecidable.
Computational Complexity Theory
Computability Theory is concerned with the question
For which decision problems do
algorithms exist
Computational Complexity Theory is concerned with the question
For which decision problems do
efficient algorithms
exist
This raises the questions:
-
What `resources' do we wish to be employed `efficiently'
-
What do we mean by `efficient'?
The two significant `resources' (or complexity measures) of interest are
TIME
and
SPACE
i.e. The number of steps an algorithm takes (in the worst-case) to return
its answer. The amount of memory needed in which to run the algorithm.
Recall that a decision problem takes as input a finite length binary string
and returns as output a 0 or a 1, hence a decision problem
f : { 0, 1 }^* -> { 0, 1 }
may be seen as an infinite sequence of
decision problems [fn], where
fn : { 0, 1 }^n -> { 0, 1 }
is the problem f limited to inputs containing exactly n bits.
We measure the running time of an algorithm as the number of steps taken
on
inputs of length n
That is, if A is an algorithm (ADA program, say) that solves a decision problem, f,
the running time of A is a
function R : N -> N, so that R( n ) is the
worst-case number of steps taken on inputs of length n.
The Time Complexity of a decision problem, f, is the running time of
the `best' algorithm A for f.
Thus we say that a decision problem, f, has
Time Complexity T( n )
if there is an an algorithm, A, for f such that
The number of steps taken by A
on inputs of length n
is always
less than or equal to T( n )
The Space Complexity of a decision problem, f, is the amount of
memory used
by the `best' algorithm A for f.
Thus we say that a decision problem, f, has
Space Complexity S( n )
if there is an an algorithm, A, for f such that
The number of memory locations used by A
on inputs of length n
is always
less than or equal to S( n )
These definitions allow us to classify decision problems according to their
Time (Space) Complexity.
Thus we can define complexity classes, e.g.
TIME ( n ) is the set of decision problems for which an algorithm running
in at most
n steps on inputs of length n exists.
TIME ( n^2 ) is the set of decision problems for which an algorithm running in at most
n^2 steps on inputs of length n exists.
TIME ( 2^n ) is the set of decision problems for which an algorithm running in at most
2^n steps on inputs of length n exists.
And in general,
TIME ( T(n) )
is
the set of decision problems
for which an algorithm
running in
at most T(n) steps
on all inputs of length n
exists.
Which complexity classes correspond to decision problems with `efficient' (for run-time)
algorithms?
Intuitively we regard an algorithm with worst-case run-time of n, n^2, n^3, etc
as being `efficient' since the time taken to return an answer for input of length n
is `acceptable' even for large values of n;
and the amount of additional computation
needed for inputs of length n+1 does not `greatly exceed' the time on inputs of length n.
On the other hand, intuitively, we would regard an algorithm with worst-case run-time of
2^n, 3^n, n^n, n, n^{logn}, etc as being `inefficient'
since even for moderate values of n the time taken to return an answer on
input of length
n is `unacceptable'; and the amount of additional computation
needed for inputs of length n+1 considerably exceeds the time on inputs of length n.
How can we distinguish run-times in the second category from run-times in the first?
All of the run-times in the first category have the following property:
For each `efficient' run-time there is a constant, k, such that the running time
is at most n^k when n is large enough.
A decision problem, f, for which there is an algorithm taking at most
n^k steps
on inputs of length n (i.e. f in TIME ( n^k )) is called a
Polynomial Time Complexity
Decision Problem
All of the run-times in the second category do not have this property, i. e.
For each `inefficient' run-time there is NO constant, k, such that
the running time
is at most n^k when n is large enough.
A decision problem, f, for which there is NO algorithm taking at most n^k steps
on inputs of length n (i.e. f is not in TIME ( n^k )) is called a
Non-Polynomial Time Complexity
Decision Problem
It is possible to show (by diagonalisation) that for
all run-time functions, T(n):
There exist decision problems, f,
such that
the Time-Complexity of f
is greater than T(n)
(thus there are decision problems which do have non-polynomial time complexity)
There are very few `natural' examples of decision problems for which such lower bounds
have been proved.
A major open problem in Computational Complexity Theory is to develop arguments
by which
important computational problems can have their time complexity described exactly.
For `almost all' `interesting' problems no lower bound on Time Complexity larger
than
OMEGA( n ) has been obtained.
Example Open Problems
We have seen that multiplication of 2 n-digit numbers has Time Complexity
at worst
n^{log3}. It is conjectured that
Multiplication is in TIME( n log n )
This conjecture remains unproven.
Multiplication of 2 n by n integer matrices can be done in time
O(N^1.81) (where N = n^2).
It is conjectured that
Matrix-Multiplication is in TIME( N log N )
Again this remains unproven.
It is unknown whether there is a polynomial time algorithm that can determine if a
given n-digit number is a Prime Number.
It is unknown whether there is a polynomial time algorithm that will factorise an
n digit number.
Computational Complexity Theory involves a large number of subfields each of which
is ultimately concerned with problems such as those above, e.g.
Algebraic Complexity Theory
Complexity of Probabilistic Algorithms
Complexity of Parallel Algorithms
Machine-Based Complexity Theory
Structural Complexity Theory
Complexity of Approximation Algorithms
Axiomatic Complexity Theory
Complexity of Counting and Enumeration
Average Case Complexity
Complexity Theory of Boolean Functions
The study of the last field is over 50 years old.
It is convenient to use a single symbol to denote the class of all
decision problems for which time efficient algorithms exist.
P = { f : f has a polynomial time algorithm }
= Union over all k TIME ( n^k )
The Complexity Class NP
Consider the following:
Composite:
Input: n-bit number, x
Output: 1 if x is a composite number; 0 otherwise.
Satisfiability: (SAT)
Input: A Boolean expression, F,
over n variables (x1,. ..,xn)
Output: 1 if the variables of F can be fixed to values which make F equal true;
0 otherwise.
Hamiltonian Cycle (HC)
Input: n-node graph, G( V, E )
Output: 1 if there is a cycle of edges in G which includes
each of
the n nodes exactly once; 0 otherwise.
CLIQUE
Input: n-node graph G( V, E ); positive integer k
Output: 1 if there is a set of k nodes, W, in V such that
every pair of nodes in W is joined by an edge in E; 0 otherwise.
3-Colourability (3-COL)
Input: n-node graph G(V,E)
Output: 1 if each node of G can be assigned one of three colours
in such a way that no two nodes joined by an edge are given the same colour;
0 otherwise.
All 5 of these (and infinitely many other) decision problems share a certain property.
They are
`Checkable' by efficient
(polynomial time) algorithms
What does this mean?
In order to solve each of the decision problems above
we have to demonstrate the existence of a particular object
which has a certain relationship to the input.
That is, to show that:
x, is composite we `only' have to find a factor of x.
F(X) is satisfiable we `only' have to find an assignment to X that
makes F true.
G(V,E) is hamiltonian we `only' have to find a suitable cycle in G.
G(V,E) has a k-clique we `only' have to find a suitable set of k nodes in V.
G(V,E) is 3-colourable we `only' have to find a suitable colouring of V
So for the examples:
Given an input instance, I, (number, Boolean expression, graph)
one has to find a witness, W (number, assignment, cycle, set of nodes, colouring)
such that a particular relationship holds between the witness and the input.
e.g.
-
That W divides I with no remainder.
-
That W makes I take the value true.
-
That W is a cycle in I containing each node of I exactly once.
-
That W is a set of k nodes in I each pair of which is connected by an edge of I.
-
That W does not assign the same colour to two nodes in I which are
joined by an edge of I.
How difficult is it to decide if something is indeed a valid witness
for instances to these decision problems?
It is easy.
One can check if :
-
W is a factor of I (by division)
-
W satisfies I (by evaluating the expression)
-
W is a hamiltonian cycle in I (by testing if I contains all
the edges in W)
-
W is a k-clique in I (test if each pair in W is joined by an edge of I)
-
W is a colouring of I (test if each edge in I joins nodes with different colours in W)
All of these can be carried out by efficient algorithms.
In summary:
-
For any decision problem, f, with each possible input size, n, there
is a set of potential witnesses Wn.
-
To solve a decision problem `all' that is needed is an algorithm to
determine if there is a genuine witness, W is in Wn for any given
input
instance I of size n.
In principle, one could do this by going through each element, W of Wn,
in turn and checking if W is a genuine witness for I.
However, the question
`Is W a genuine witness for I'
(for the decision problem f)
(e.g.
-
Is y a factor of x? (for Composite)
-
Does alpha make F(X) equal true? (for SAT)
-
Is C a hamiltonian cycle in G(V,E)? (for HC)
-
Is K a k-clique in G(V,E) (for Clique)
-
Is chi is 3-colouring of G(V,E) (for 3-Col) )
-
is itself a decision problem (based on f)
So for any decision problem, f, we can define another decision
problem, CHECK(f)
CHECK(f):
Input: I input instance for f; W possible witness that f(I)=1.
Output: 1 if W is a genuine witness that f(I)=1;
0 otherwise
Now we have seen that
-
CHECK(Composite)
-
CHECK(SAT)
-
CHECK(HC)
-
CHECK(Clique)
-
CHECK(3-Col)
are all polynomial time decidable, i.e. all of these have efficient algorithms.
The notation, NP, denotes the class of all decision problems, f, with the
property that CHECK(f) is polynomial time decidable,
NP = { f : CHECK(f) is in P }
Thus for decision problems we have two `variants'
Finding version of f
(f itself)
which asks
Is there any witness W for I (with f)
and
Verifying version of f
(Check(f))
which asks
Is this specific W a witness for I (with f)
P is the class of problems with efficient `finding' algorithms.
NP is the class of problems with efficient `verifying' algorithms.
How are P and NP related?
If f is in P then certainly Check(f)
is in P and so f is in NP also.
Thus,
P is a subset of NP
Undoubtedly the most important open question in modern Computational Complexity
Theory is:
Is P a proper subset of NP?
i.e.
Are there decision problems f
such that Check(f) is in P (i.e. f is in NP) but
for which f is not in P.
Or, in informal terms,
Are there decision problems f such that checking a solution (witness) is
much easier (polynomial time) than finding a solution?
The following problems are a fraction of the tens of thousands of problems which
are known to be in NP but for which no efficient algorithm has been found
(despite, in some cases, centuries of work on them)
- Hamiltonian Cycle
-
Satisfiability
-
3-Colouring
-
Clique
-
Travelling Salesman Problem
-
Integer Knapsack Problem
-
Longest Path in a Graph
-
Edge Colouring
-
Optimal Scheduling
-
Minimising Boolean Expressions
-
Minimum Graph Partition
-
Composite Number
-
Primality
With the exception of the last 2, it is generally believed that no efficient algorithm
exists for any of these decision problems.
i.e. They are all intractable.
This has yet to be proved.
The concept of NP-complete decision problems offers a possible route
to resolving whether P = NP or P = NP.
NP-completeness
The idea underlying the concept of NP-complete problems
is to describe formally what can be understood as the
`most difficult' problems in NP
That NP-complete problems are (intuitively) the most difficult
in NP follows from the fact that we may prove
P = NP
if and only if
some NP-complete problem, f,
has a polynomial-time algorithm
Suppose S and T are two decision problems and suppose we can
construct an ADA program (algorithm) to solve T that is of
the form
procedure T is
x : T_input_type;
y : S_input_type;
function S ( z : S_input_type)
return boolean is
--***************************************
-- ADA function for decision problem S
-- goes in here.
--***************************************
end S;
function transform ( t : T_input_type)
return S_input_type is
--*****************************************
-- ADA function which transforms an
-- input instance for T into an input
-- instance for S.
--*****************************************
end transform;
begin
get (x);
y := transform (x);
if S(y) then
put (1);
else
put (0);
end if;
end T;
In this transform is a function which takes an input instance for T
and changes it into an input instance for S. For example if T is a
decision
problem on numbers and S is one on graphs, then transform given a
number would construct a graph using that number.
Now suppose that both:
transform and S
have efficient (polynomial)
algorithms
Then the procedure above gives an efficient algorithm for T.
It follows that (with the above procedure form)
There is an efficient algorithm for T
if
there is an efficient algorithm for S
But, more importantly,
If we can prove that there is
NO efficient algorithm for S
then
we have also proved that there is
NO efficient algorithm for T
This means that if we have of an efficient procedure, tau which
-
transforms input instances x for T into input instances, tau( x), for S
-
is such that T( x ) = 1 if and only if S( tau( x ) ) = 1
Then we have established a relationship between the Time-Complexity of S and the Time-Complexity
of T.
If S and T are decision problems for which such an efficient transformation procedure
from inputs for T to inputs for S exists then we say that
The decision problem T is
polynomially reducible
to the decision problem S
This relationship is denoted
T < =p S
How does the idea of `polynomial reducibility' help in addressing the question
of whether P equals NP?
Suppose we have a decision problem, f, for which we can prove the following:
-
f is in NP, i.e. f there is an efficient checking algorithm for f.
-
For every other decision problem, g in
NP, it is the case that g < =p f,
i.e. for
every decision problem, g with an efficient checking algorithm there is an efficient procedure,
tau-g, that transforms inputs for g into inputs for f.
Then if there are decision problems in NP for which efficient algorithms do not exist
then
the decision problem f must be
one such problem
In other words, for such a decision problem f:
P = NP
if and only if
f has an efficient algorithm (i.e. f is in P)
A decision problem, f, which has these properties, i.e.
-
f is in NP
-
For all g in NP, g < =p f
(f has an efficient checking algorithm and every problem with an efficient checking algorithm
can be efficiently transformed to f)
is called an
NP-complete decision problem
The NP-complete decision problems are the `most difficult' problems in NP in the sense
that if
Any single NP-complete problem does not
have an efficient algorithm
then
NO NP-complete problem
has an efficient algorithm
Conversely
If we find an efficient algorithm for
just one NP-complete problem
then
we can construct efficient algorithms
for all
decision problems in NP
Problem:
The definition of NP-completeness requires the following to be done in order
to show that a problem f is NP-complete
-
We have to find an efficient checking algorithm for f (i.e. prove f is in NP)
-
We have to show that every problem with an efficient checking algorithm can be
transformed into f (i.e. prove for all g in NP, g < =p f)
The first is usually (relatively) easy.
But for the second, how can we reduce infinitely many decision problems to a
single problem?
Before dealing with this we can note the following: suppose we have shown
for two decision problems, f and g say, that:
-
f is NP-complete.
-
g is in NP
-
f < =p g
Then we have also shown that g is NP-complete.
Why?
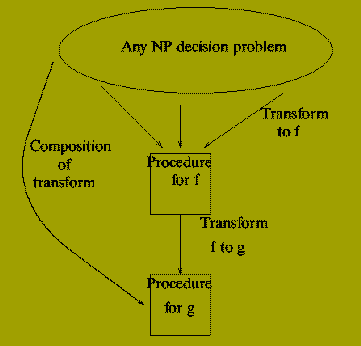
So we have a polynomial reduction from every problem in NP to g by
-
Converting an input instance x for h (in NP) to one tau(h)(x) for f.
-
Converting the input tau(h)(x) for f to an input instance for g.
The first is possible since f is NP-complete. The second since there is a polynomial
reduction from f to g.
This argument shows that once we have identified a single NP-complete
decision problem, f, in order to prove that another decision problem, g, is
NP-complete `all' we have to do is find an efficient algorithm for transforming
input instances for f into input instances for g, i.e. prove
f < =p g
But, this still leaves the problem of finding a `first' NP-complete problem, that is
of finding some way of
transforming infinitely many
decision problems
into
just one
decision problem
In 1971 Steven Cook proved one of the most important results in modern computational
complexity theory. This result is (now) known as
Cook's Theorem
SAT is NP-complete
Proof: See next section.
Within a few months of Cook's result dozens of new NP-complete problems had
been identified. By 1994 well over 10,000 basic NP-complete decision problems
were known.
Thus it is known that the following problems are all NP-complete
- CLIQUE
-
Hamiltonian Cycle
-
Travelling Salesman Problem
-
3-Colouring
-
Set Partitioning
-
Edge Colouring
-
Longest Path
-
Integer Knapsack
A proof that a decision problem is NP-complete is accepted as evidence that
the problem is intractable since a fast method of solving a single NP-complete
problem would immediately give fast algorithms for all NP-complete
problems.
It generally though to be extremely unlikely that any NP-complete
problem has a fast algorithm.
It has still to be proved that any NP-complete problem does not have
an efficient algorithm, i.e. the question of whether P=NP is still open.
While most of the classical decision problems have now been determined as
being in P or being NP-complete a number of important problems are
still open. In particular
Primality
Composite Number
Both are known to be in NP. Neither has been shown to be NP-complete. It is
believed that both are in fact solvable by efficient algorithms.
Non-deterministic Ada Programs
A program can alter one `bit' of memory at a time.
The current bit is indexed by an integer value: at_cell
The next bit is always adjacent to the previous one.
The program is in one of a finite number, s say, of states.
The next state entered is chosen non-deterministically from a choice of
two.
A complete program is specified when the action for each state and bit value
is defined.
State s is the unique accept state.
procedure nd_ada_f (T:integer) is
type workspace is array (integer range <>) of 01B;
n : integer;
begin
get(n);
declare
w : workspace( -T..T ):=(others=>B);
procedure do_it_on ( w : in out workspace;
position : in out integer;
state : in out integer);
begin
case state is
when k =>
if w(position)=B then
w(position):=(0 or 1)k; position:=position (+-1)k;
state:=choose(next1, next2)k;
elsif w(position)=0 then
w(position):=(0 or 1)k; position:=position (+-1)k;
state:=choose(next1, next2)k;
else
w(position):=(0 or 1)k; position:=position (+-1)k;
state:=choose(next1, next2)k;
end if;
end case;
end do_it_on;
begin
at_cell:=1; in_state:=1; get(w(1..n));
for i in 1.. T loop
do_it_on(w,at_cell,in_state);
end loop;
if in_state=accept then return true; end if;
end;
end nd_ada_f;
The decision problem NCOMP is:
Input:
A non-deterministic program, AP;
An input x in <0,1>n for AP;
A time bound T.
Question: Is there a `computation path' of AP on x that
accepts in T iterations?
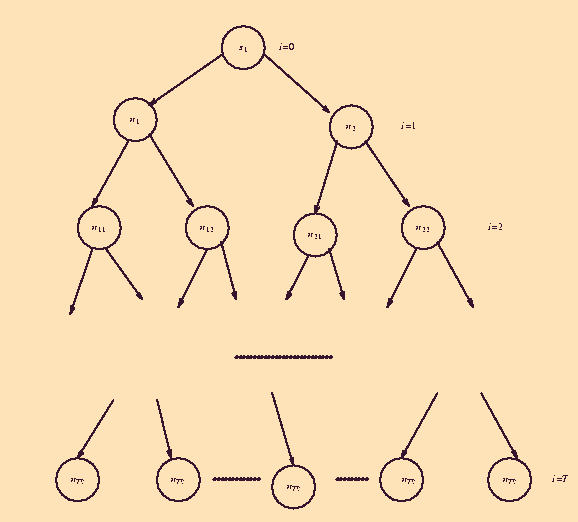
Computation Tree
An Alternative to NP
ADA_NP is the class of decision problems, f, for which there are:
-
A non-deterministic Ada program, NA, and
-
A polynomial p(n)
that satisfy:
-
For all x in {0,1}n such that f(x)=1,
NCOMP( NA,x,p(n))=1
Theorem: ADA_NP=NP
Proof:
a) ADA_NP is a subset of NP.
Suppose that f is in ADA_NP.
Let NAf and p(n) be the program and polynomial such that for all x in {0,1}n:
f(x)=1 if and only if NCOMP(NAf, x, p(n))=1
A set of witnesses to f(x)=1 is the set of computation paths NACP,
for NAf.
Checkf(CP,x)=1 if CP is a valid accept computation for
NAf on input x.
Given NAf, CP and x this can
be checked by simulating NAf on x using the computation path CP.
This test can be done in polynomial-time, so Checkf is in P, i.e.
f is in NP.
b) NP is a subset of ADA_NP
Let f is in NP, so that Checkf is in P.
Let Wn be the witness set for x in {0,1}n.
For any w in Wn it must hold that |w|<= p(n) for some polynomial p(n).
(otherwise Checkf(x,w) could not be carried out in P).
Let Wn be encoded in binary. Then
For all x in {0,1}n
there are at most 2p(n) `witnesses to f(x)=1'.
NAf is the program which:
-
In its first p(n) iterations
generates each w in Wn on some computation path.
-
In the next q(n) iterations runs the
Checkf(x,w) algorithm (reaching accept iff
Checkf(x,w)=1).
NCOMP(NAf,x,p(n)+q(n))=1 if and only if NAf has a
path of length p(n)+q(n) ending in accept on input x.
iff NAf constructs a witness w for x after p(n) moves
which checks correctly in q(n) steps
iff Checkf is in P.
In summary, Checkf in P implies that f is in ADA_NP.
Hence (from (a) and (b)), ADA_NP=NP.
The Satisfiability Problem (SAT) is:
Input: A set of n Boolean variables
Xn=<^x1,x2,...,xn>;
A Boolean formula F over Xn,
(whose length is at most r(n) for some polynomial r)
Question: Is there an assignment, a of true/false to the variables Xn
with the property that F(a)=true?
Cook's Theorem
SAT is NP-complete.
Proof:
We have to do 2 things:
-
Prove that SAT belongs to NP;
-
Show that for any decision problem f in NP: f<=pSAT:
i.e. Any instance x of f can
be transformed into an instance F(x) of SAT such that f(x)=1 iff SAT (F(x))=1.
That (a) holds has already been shown.
Now let f be any decision problem in NP.
We know that f also belongs to ADA_NP (since NP=ADA_NP).
So there is a non-deterministic Ada program NAf for
f and a polynomial p(n) such that,
for any x in {0,1}n,
f(x)=1 iff NCOMP( NAf,x,p(n))=1
To show that SAT is NP-complete, we build an instance of SAT
(i.e. a Boolean formula), H (NAf) (Xm(n))
with the property
H(NAf)(Xm(n)) is satisfiable
iff
NCOMP(NAf,x,p(n))=1.
What do we know about NAf on input x in {0,1}n?
At any value i of its main for loop its status is fully described by
A1) The value of in_state.
A2) The value of at_cell.
A3) The content (0, 1, or B) of each `bit' w(k).
These can change only in accordance with
what the procedure do_it_on allows, given the
initial n-bit input x.
So, suppose we wish to know if a given sequence of p(n) configurations (i.e. state, position, memory)
is a valid accepting computation path on NAf.
Then such a sequence must embody all of the following characteristics at all times i:
C1) At time i=0: in_state=1, w(1..n)=x, all other bits
equal B; at_cell=1.
C2) in_state has exactly one value at time i.
C3) at_cell has exactly one value at time i.
C4) w(k) has exactly one value at time i, (for all k)
C5) in_state=s (accept state) at i=p(n).
C6) w(-p(n)...p(n)), at_cell, and in_state must change
from time i to time i+1 according to the case statement in do_it_on of
NAf.
We construct H(NAf) with the Boolean variables:
(below 0 <= i <= p(n))
V1) 3(2p(n)+1)(p(n)+1) variables
W(v,k,i) with v in {0,1,B}, -p(n) <= k <= p(n)
V2) s(p(n)+1) variables
S(st,i) 1 <= st <= s,
V3) (2p(n)+1)(p(n)+1) variables
A(k,i) -p(n) <= k <= p(n)
H(NAf(x)) is built so that:
in a satisfying assignment those
variables which which are assigned the value true define a valid computation, CP
of NAf on x:
V1T) W(v,k,i)=1 iff
in CP: at time i, `bit' w(k) contains v.
V2T) S(st,i)=1 iff in CP: at time i, in_state=st.
V3T) A(k,i)=1 iff in CP: at time i, at_cell=k.
Thus the whose only satisfying assignments of H(NAf)(V1,V2,V3)
will be as given by (V1T, V2T, V3T) and
define legal computations of NAf
on x, i.e. capture the conditions (C1) through (C6)
(Below & denotes logical and; + denotes logical or.
For brevity we assume and is implied).
C1)
S(1,0)A(1,0) &k=1n W( xi,k,0) &
&k=-p(n)0 W(B,k,0) &k=n+1p(n) W(B,k,0)
C2) `exactly one value' == `at least one value'
and at most one value.
&i=0p(n)( +st=1s S(st,i) ) &
&1<=c< d<=s (-S(c,i) + -S(d,i))
C3) Similarly,
&i=0p(n) ( +k=-p(n)p(n) A(k, i) ) &
&-p(n) <=c< d<=p(n) ( -A(c,i) + -A(d,i) )
C4) Again, similarly,
&i=0p(n) &k=-p(n)p(n) ( +{v in {0,1,B } W(v,k,i) )
&v1=v2 ( -W( v1,k,i) + -W( v2,k,i) )
C5) S(s,p(n))
C6) is, superficially, more complicated, however at time i: from
in_state=st, at_cell=k, w(k) is one of {0,1,B}
the case
statement determines the values at time i+1 of
the new value of at_cell
the content of w(k),
the two possible next states to jump to.
Thus each of the s states is described by a `move' function:
delta (st,v) = ( ( st1 , st2 ), nv, ch )
where v is in {0,1,B}, nv is in {0,1}, ch=(+or-)1
We thus have (C6) as
&i=1p(n)-1 &j=-p(n)p(n) &{delta (st,v)}
MOVE(i,j,st,v, st1 , st2,nv,ch)
where
MOVE(i,j,st,v, st1, st2, nv , ch) is,
S(st,i)& A(j,i)& W(v,j,i) ->
( S( st1,i+1) & A(j+ch,i+1) & W(nv,j,i+1) +
S( st2,i+1) & A(j+ch,i+1) & W(nv,j,i+1) )
Thus,
If at time i
NAf is in_state st
at_cell j which contains v then
at time i+1,
NAf is in_state st1 or st2
at_cell j+ch with cell j containing nv.
So the final formula H(NAf) (V1,V2,V3) is
C1 & C2 & C3 & C4 & C5 & C6 ( V1,V2,V3 )
H(NAf)(V1,V2,V3) is satisfiable
iff
NCOMP (NAf,x,p(n))=1.
If NCOMP( NAf,x, p(n))=1 setting
the variables of V1, V2, V3 that encode the
accepting computation path of NAf gives a satisfying assignment of H;
H guarantees that the true variables
of any satisfying assignment must represent a valid computation of
NAf on input x that ends in accept after p(n) steps.
i.e. a witness that NCOMP ( NAf, x, p(n) )=1