
The discussion above has, casually, assumed that there are decision problems for which algorithms do not exist.
(nothing above has given any evidence for the assumption made).
We can prove that there exist decision problems for which no algorithm exists by employing a method of argument called
If there are `more' decision problems than programs then it must be the case that some decision problems cannot be solved by programs since since a single program can solve only a single decision problem.
Suppose we are given two sets of items, A and B, say, e.g.
A = Set of all students registered for the course 2CS46
B = Set of all students registered for the course 2CS42
How can we tell if there are more items in A than there are in B?
By `counting' the number of items in each set.

Thus there are an infinite number of distinct decision problems.
How many different ADA programs are there which take a single number, n, as input and return a 0 or 1 as their result?
Infinitely many. Since there are clearly infinitely many such programs which contain a loop of the form
for i in 1..m loop
s := 0;
end loop;
`Counting' is all right when the sets being compared are finite.
`Counting' does not appear to tell us anything when both sets are infinite.
Q: What do we actually do when we `count' the number of items in a set?
A: To each item we attach a unique `label': 1,2,3,4,...
Thus, in comparing the sizes of two finite sets, A and B, we attach `labels' to the items in A, and `labels' to the items in B and we say that
But why use `numbers' as the `labels' to count with?
We could use items in A to label items in B (i.e. count) and, if A is larger than B, then at least one item in A will not have been used to label any item in B.

And we can `count' B by using the `labels'
and now GARY has not been used to label any element of B and so we can say that
If it can be shown that for every way of labelling items in B with items in A there is at least one item of A which is not used as a label then, again, we can state that:
Let:
A = The set of all decision problems, f : N -> {0,1}.
B = The set of all ADA programs.
We can enumerate (i.e. list) every single ADA program. That is there is an algorithm which will output every single different ADA program in turn, e.g.
i := 1;
loop
if ADA_PROGRAM ( i ) = 1 then
put ( Binary representation of i );
end if;
i :=i + 1;
end loop;
(Recall that ADA_PROGRAM ( n ) is the decision problem which tests if n
written in binary corresponds to the ASCII character representation of a compiling
ADA program)
Thus we can talk about a
i.e. the 1st, 2nd, 3rd, ..., nth, ..., program that is output by the procedure above.
And so we can form an infinite table, T:
| 1 | 2 | 3 | ........ | n | ........ | |
|---|---|---|---|---|---|---|
| P1 | *P1 (1) | P1 (2) | P1(3) | ........ | P1(n) | ........ |
| P2 | P2 (1) | *P2 (2) | P2 (3) | ........ | P2 (n) | ........ |
| P3 | P3 (1) | P3 (2) | *P3 (3) | ........ | P3 (n) | ........ |
| .. | .. | .. | .. | ........ | ||
| .. | .. | .. | .. | ........ | ||
| Pn | Pn (1) | Pn (2) | Pn (3) | ........ | *Pn (n) | ........ |
| .. | .. | .. | .. | ........ | ||
| .. | .. | .. | .. | ........ |
If it is the case that every decision problem, f, is computed by at least one ADA program, then in the table above which `labels' each ADA program with a decision problem:
i.e. There is a row, Pf, of the table such that Pf( n ) = f( n ) for all n.
What about the following decision problem?
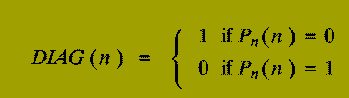
DIAG is well-defined, since our table, T, above exists.
P1 (DIAG(1) /= P1(1))
OR that labelling P2 (DIAG(2) /= P2(2))
OR that labelling P3 (DIAG(3) /= P3(3))
...
OR that labelling Pn (DIAG(n) /= Pn(n)).
And so, the decision problem, DIAG, does not label any Pn, in the table T.
Now matter how the ADA programs are ordered, we can always define a decision problem, DIAG, as above, which does not label any program in the ordering.
In consequence:
Decision problems for which no algorithm exists are called: