Complexity Theory - NP and NP-completeness
NP and NP-completeness
The Complexity Class NP
Consider the following:
Composite:
Input: n-bit number, x
Output: 1 if x is a composite number; 0 otherwise.
Satisfiability: (SAT)
Input: A Boolean expression, F,
over n variables (x1,. ..,xn)
Output: 1 if the variables of F can be fixed to values which make F equal true;
0 otherwise.
Hamiltonian Cycle (HC)
Input: n-node graph, G( V, E )
Output: 1 if there is a cycle of edges in G which includes
each of
the n nodes exactly once; 0 otherwise.
CLIQUE
Input: n-node graph G( V, E ); positive integer k
Output: 1 if there is a set of k nodes, W, in V such that
every pair of nodes in W is joined by an edge in E; 0 otherwise.
3-Colourability (3-COL)
Input: n-node graph G(V,E)
Output: 1 if each node of G can be assigned one of three colours
in such a way that no two nodes joined by an edge are given the same colour;
0 otherwise.
All 5 of these (and infinitely many other) decision problems share a certain property.
They are
`Checkable' by efficient
(polynomial time) algorithms
What does this mean?
In order to solve each of the decision problems above
we have to demonstrate the existence of a particular object
which has a certain relationship to the input.
That is, to show that:
x, is composite we `only' have to find a factor of x.
F(X) is satisfiable we `only' have to find an assignment to X that
makes F true.
G(V,E) is hamiltonian we `only' have to find a suitable cycle in G.
G(V,E) has a k-clique we `only' have to find a suitable set of k nodes in V.
G(V,E) is 3-colourable we `only' have to find a suitable colouring of V
So for the examples:
Given an input instance, I, (number, Boolean expression, graph)
one has to find a witness, W (number, assignment, cycle, set of nodes, colouring)
such that a particular relationship holds between the witness and the input.
e.g.
-
That W divides I with no remainder.
-
That W makes I take the value true.
-
That W is a cycle in I containing each node of I exactly once.
-
That W is a set of k nodes in I each pair of which is connected by an edge of I.
-
That W does not assign the same colour to two nodes in I which are
joined by an edge of I.
How difficult is it to decide if something is indeed a valid witness
for instances to these decision problems?
It is easy.
One can check if :
-
W is a factor of I (by division)
-
W satisfies I (by evaluating the expression)
-
W is a hamiltonian cycle in I (by testing if I contains all
the edges in W)
-
W is a k-clique in I (test if each pair in W is joined by an edge of I)
-
W is a colouring of I (test if each edge in I joins nodes with different colours in W)
All of these can be carried out by efficient algorithms.
In summary:
-
For any decision problem, f, with each possible input size, n, there
is a set of potential witnesses Wn.
-
To solve a decision problem `all' that is needed is an algorithm to
determine if there is a genuine witness, W is in Wn for any given
input
instance I of size n.
In principle, one could do this by going through each element, W of Wn,
in turn and checking if W is a genuine witness for I.
However, the question
`Is W a genuine witness for I'
(for the decision problem f)
(e.g.
-
Is y a factor of x? (for Composite)
-
Does alpha make F(X) equal true? (for SAT)
-
Is C a hamiltonian cycle in G(V,E)? (for HC)
-
Is K a k-clique in G(V,E) (for Clique)
-
Is chi is 3-colouring of G(V,E) (for 3-Col) )
-
is itself a decision problem (based on f)
So for any decision problem, f, we can define another decision
problem, CHECK(f)
CHECK(f):
Input: I input instance for f; W possible witness that f(I)=1.
Output: 1 if W is a genuine witness that f(I)=1;
0 otherwise
Now we have seen that
-
CHECK(Composite)
-
CHECK(SAT)
-
CHECK(HC)
-
CHECK(Clique)
-
CHECK(3-Col)
are all polynomial time decidable, i.e. all of these have efficient algorithms.
The notation, NP, denotes the class of all decision problems, f, with the
property that CHECK(f) is polynomial time decidable,
NP = { f : CHECK(f) is in P }
Thus for decision problems we have two `variants'
Finding version of f
(f itself)
which asks
Is there any witness W for I (with f)
and
Verifying version of f
(Check(f))
which asks
Is this specific W a witness for I (with f)
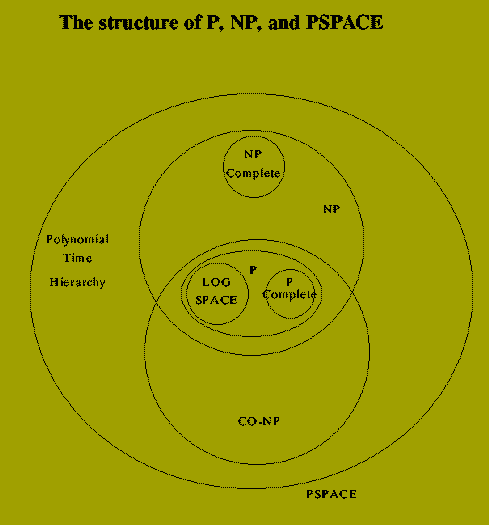
P is the class of problems with efficient `finding' algorithms.
NP is the class of problems with efficient `verifying' algorithms.
How are P and NP related?
If f is in P then certainly Check(f)
is in P and so f is in NP also.
Thus,
P is a subset of NP
Undoubtedly the most important open question in modern Computational Complexity
Theory is:
Is P a proper subset of NP?
i.e.
Are there decision problems f
such that Check(f) is in P (i.e. f is in NP) but
for which f is not in P.
Or, in informal terms,
Are there decision problems f such that checking a solution (witness) is
much easier (polynomial time) than finding a solution?
The following problems are a fraction of the tens of thousands of problems which
are known to be in NP but for which no efficient algorithm has been found
(despite, in some cases, centuries of work on them)
- Hamiltonian Cycle
-
Satisfiability
-
3-Colouring
-
Clique
-
Travelling Salesman Problem
-
Integer Knapsack Problem
-
Longest Path in a Graph
-
Edge Colouring
-
Optimal Scheduling
-
Minimising Boolean Expressions
-
Minimum Graph Partition
-
Composite Number
-
Primality
With the exception of the last 2, it is generally believed that no efficient algorithm
exists for any of these decision problems.
i.e. They are all intractable.
This has yet to be proved.
The concept of NP-complete decision problems offers a possible route
to resolving whether P = NP or P = NP.
NP-completeness
The idea underlying the concept of NP-complete problems
is to describe formally what can be understood as the
`most difficult' problems in NP
That NP-complete problems are (intuitively) the most difficult
in NP follows from the fact that we may prove
P = NP
if and only if
some NP-complete problem, f,
has a polynomial-time algorithm
Suppose S and T are two decision problems and suppose we can
construct an ADA program (algorithm) to solve T that is of
the form
procedure T is
x : T_input_type;
y : S_input_type;
function S ( z : S_input_type)
return boolean is
--***************************************
-- ADA function for decision problem S
-- goes in here.
--***************************************
end S;
function transform ( t : T_input_type)
return S_input_type is
--*****************************************
-- ADA function which transforms an
-- input instance for T into an input
-- instance for S.
--*****************************************
end transform;
begin
get (x);
y := transform (x);
if S(y) then
put (1);
else
put (0);
end if;
end T;
In this transform is a function which takes an input instance for T
and changes it into an input instance for S. For example if T is a
decision
problem on numbers and S is one on graphs, then transform given a
number would construct a graph using that number.
Now suppose that both:
transform and S
have efficient (polynomial)
algorithms
Then the procedure above gives an efficient algorithm for T.
It follows that (with the above procedure form)
There is an efficient algorithm for T
if
there is an efficient algorithm for S
But, more importantly,
If we can prove that there is
NO efficient algorithm for S
then
we have also proved that there is
NO efficient algorithm for T
This means that if we have of an efficient procedure, tau which
-
transforms input instances x for T into input instances, tau( x), for S
-
is such that T( x ) = 1 if and only if S( tau( x ) ) = 1
Then we have established a relationship between the Time-Complexity of S and the Time-Complexity
of T.
If S and T are decision problems for which such an efficient transformation procedure
from inputs for T to inputs for S exists then we say that
The decision problem T is
polynomially reducible
to the decision problem S
This relationship is denoted
T < =p S
How does the idea of `polynomial reducibility' help in addressing the question
of whether P equals NP?
Suppose we have a decision problem, f, for which we can prove the following:
-
f is in NP, i.e. f there is an efficient checking algorithm for f.
-
For every other decision problem, g in
NP, it is the case that g < =p f,
i.e. for
every decision problem, g with an efficient checking algorithm there is an efficient procedure,
tau-g, that transforms inputs for g into inputs for f.
Then if there are decision problems in NP for which efficient algorithms do not exist
then
the decision problem f must be
one such problem
In other words, for such a decision problem f:
P = NP
if and only if
f has an efficient algorithm (i.e. f is in P)
A decision problem, f, which has these properties, i.e.
-
f is in NP
-
For all g in NP, g < =p f
(f has an efficient checking algorithm and every problem with an efficient checking algorithm
can be efficiently transformed to f)
is called an
NP-complete decision problem
The NP-complete decision problems are the `most difficult' problems in NP in the sense
that if
Any single NP-complete problem does not
have an efficient algorithm
then
NO NP-complete problem
has an efficient algorithm
Conversely
If we find an efficient algorithm for
just one NP-complete problem
then
we can construct efficient algorithms
for all
decision problems in NP
Problem:
The definition of NP-completeness requires the following to be done in order
to show that a problem f is NP-complete
-
We have to find an efficient checking algorithm for f (i.e. prove f is in NP)
-
We have to show that every problem with an efficient checking algorithm can be
transformed into f (i.e. prove for all g in NP, g < =p f)
The first is usually (relatively) easy.
But for the second, how can we reduce infinitely many decision problems to a
single problem?
Before dealing with this we can note the following: suppose we have shown
for two decision problems, f and g say, that:
-
f is NP-complete.
-
g is in NP
-
f < =p g
Then we have also shown that g is NP-complete.
Why?
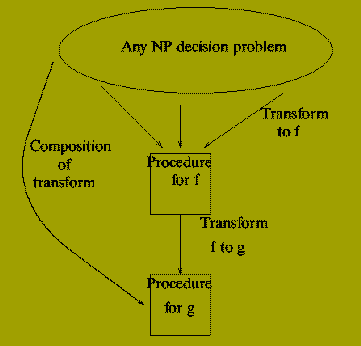
So we have a polynomial reduction from every problem in NP to g by
-
Converting an input instance x for h (in NP) to one tau(h)(x) for f.
-
Converting the input tau(h)(x) for f to an input instance for g.
The first is possible since f is NP-complete. The second since there is a polynomial
reduction from f to g.
This argument shows that once we have identified a single NP-complete
decision problem, f, in order to prove that another decision problem, g, is
NP-complete `all' we have to do is find an efficient algorithm for transforming
input instances for f into input instances for g, i.e. prove
f < =p g
But, this still leaves the problem of finding a `first' NP-complete problem, that is
of finding some way of
transforming infinitely many
decision problems
into
just one
decision problem
In 1971 Steven Cook proved one of the most important results in modern computational
complexity theory. This result is (now) known as
Cook's Theorem
SAT is NP-complete
Proof: Omitted (not difficult, just long)
Within a few months of Cook's result dozens of new NP-complete problems had
been identified. By 1994 well over 10,000 basic NP-complete decision problems
were known.
Thus it is known that the following problems are all NP-complete
- CLIQUE
-
Hamiltonian Cycle
-
Travelling Salesman Problem
-
3-Colouring
-
Set Partitioning
-
Edge Colouring
-
Longest Path
-
Integer Knapsack
A proof that a decision problem is NP-complete is accepted as evidence that
the problem is intractable since a fast method of solving a single NP-complete
problem would immediately give fast algorithms for all NP-complete
problems.
It generally though to be extremely unlikely that any NP-complete
problem has a fast algorithm.
It has still to be proved that any NP-complete problem does not have
an efficient algorithm, i.e. the question of whether P=NP is still open.
While most of the classical decision problems have now been determined as
being in P or being NP-complete a number of important problems are
still open. In particular
Primality
Composite Number
Both are known to be in NP. Neither has been shown to be NP-complete. It is
believed that both are in fact solvable by efficient algorithms.
 PED Home Page
PED Home Page


