Mechanical Aids to Computation and the Development of Algorithms

Dr. Paul E. Dunne

Dept. of Computer Science

(Room 3.10, Chadwick Tower)

e-mail ped@uk.ac.liv.csc

Introduction

Popular Beliefs

Computers can do anything

A `mathematical refutation' of this was given in 1936 by Alan Turing: computers can only manipulate strings of symbols. If a task can be expressed as a sequence of operations on a collection of symbol strings then a computer may be programmed to perform the task. It may be proved that certain tasks cannot be expressed in this way.

Computers make mistakes

Computers are inanimate tools used by individuals. People make mistakes not machines.

Computers threaten/benefit society

This is a view that has been held about almost all new inventions, discoveries, technologies. For example

For the specific case of computers a common source of both utopian and dystopian views is through cinema depictions, e.g.

Computers are intelligent

This common belief is based on fallacious reasoning promoted by non-Computer Scientists and some Computer Science `experts'. Namely

Computers affect people's lives

One of the areas in which computer systems have become predominant in the last 20 years is that of

Record storage and maintenance

Thus, in many areas, information on individuals is held on computer databases

The widespread use of such sytems has caused concern on the grounds of Some of these concerns have been addressed in 2 Acts of Parliament, passed since 1984. The Data Protection Act (1984) One consequence has been the adoption of the practise of releasing exam marks to students at the University of Liverpool.

The Computer Misuse Act (1990)

A Private Member's Bill sponsored by the Consertative M.P., Emma Nicholson.

What are Current Concerns

in Computer Science

We look at 3 areas (this is not exhaustive)

Artificial Intelligence

First mooted by Alan Turing. Properly began in the mid-1950s with the work of Minsky, McCarthy and others in the U.S. Two main schools of thought:

(A) has made little progress, although recently it has provided a stimulus for interaction between Computer Science, Psychology, and Linguistics.

(B) has had some success in the area of Expert Systems.

Non-traditional Computers

(non-von Neuman machines)

A number of different subfields fall into this category:

(1) uses ideas from physiological models of the brain as a computing paradigm. (2) exloits ideas from Biology and D.N.A. evolution. (3) uses models from Quantum Physics as a computational approach. (4) encompasses the first three and deals with the issue of designing machines in which large numbers of computers operate together.

Mathematical Theory of Computation

Arguably the oldest area of Computer Science. There are three main areas of research.

(1) is concerned with the issue of devising calculi by which programs may be mathematically proved to be correct. (2) dates from 1900. It deals with the issue of what problems can be solved by computers and which can be proven impossible to solve. (3), in various forms, dates back to the 1930s. It is concerned with the question of which problems can be solved efficiently by computer systems.

Lecture 2

Early Development of Algorithms and Mechanical Counting Aids

Many of the concerns underlying modern computer systems date back to the earliest civilisations. Computers manipulate data to produce a desired result i.e. They transform given representations of information. There are two important concepts in this description:

The first deals with how specific items of information may be described in a `universally' recognised form. The second deals with the procedures (programs or algorithms) which are used to transform such representations to produce a result. An example of the second is the method taught in schools for carrying out long multiplication. Why, given a common means of representing information (e.g. numbers), and procedures for manipulating such representations (e.g. multiplying, adding), does one want to have mechanical help with performing the calculations? Becuase such calculations as arise in practise are often involved and laborious. Hence, e.g. How would you prefer to calculate 123478474 times 6772366367? Would you trust an answer that had been produced by hand using long multiplication? The development of computational methods involved three areas:

Number Representation

The influence of these two systems survives today, e.g. time measurement; angular measurement.

This used a symbol represent the number 0. (also a Mayan discovery)

Employed a positional notation.

Used 10 different symbols to represent the numbers 0 through 9

First popularised in Europe by Leonardo of Pisa in his Liber Abaci (The Book of Computation) of 1228.

Early Computing Devices

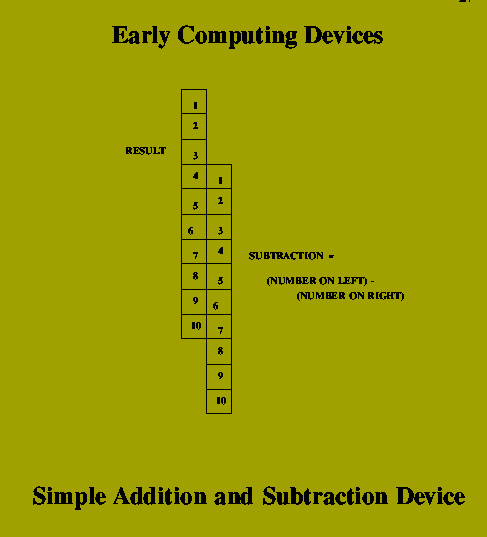
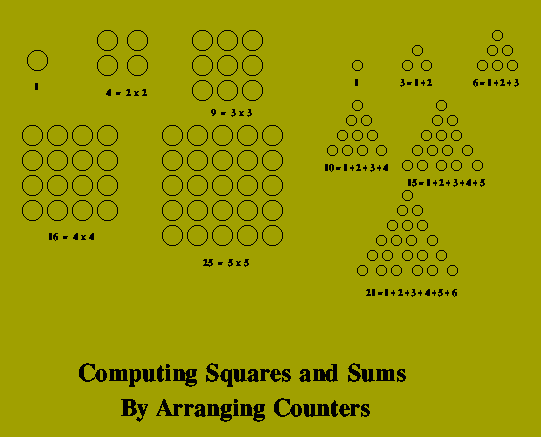
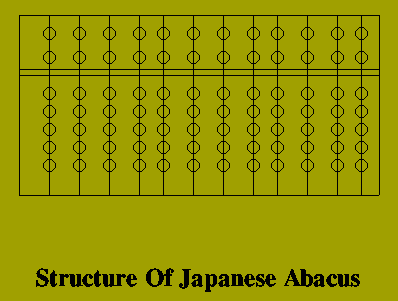
Euclid's concept of Algorithm

The Greek mathematician, Euclid (4th Century B.C) is the earliest known identifier of specific algorithms Euclid's work The Elements is of collection of results, mainly in Geometry.

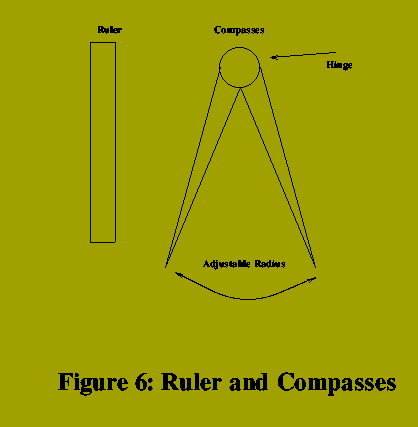
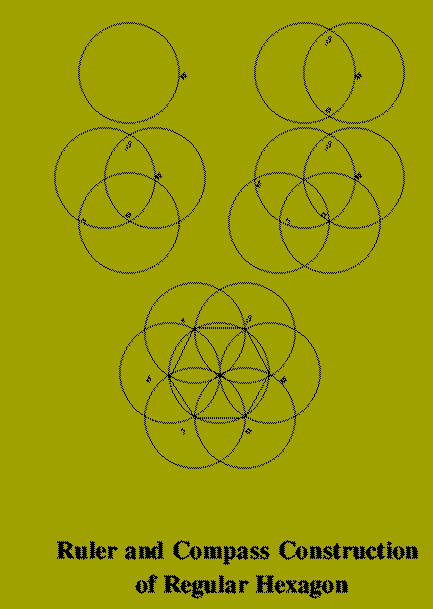
Although this may seem a very primitive class of algorithm, problems of great subtlety arise in it. 3 classical problems were not solved until over 2000 years after Euclid's death: 

greatest common divisor of m and n

1. If m is smaller than n then 
         swop the values of m and n.
2. Set m equal to the remainder of 
         m divided by n.
3. If m is not equal to 0 then 
         go back to step 1, with the
         new values of n and m.
4. Return n as the answer.

.sp

Euclid's Algorithm Euclid's work was not the only early investigation of algorithms. Another important Greek contribution concerns a problem which is still very much of interest today em the generation of prime numbers. The first algorithm to identify prime numbers is the famous Sieve of Eratosthenes (fl. 3rd Century B.C). Write down all the numbers from 2 to n and then carry out the following steps: 

1. Let k := 2
2. For each number, m, between k+1 and n 
         if m is an exact multiple of k then 
         cross m of the list of numbers.
3. Set k to be the smallest uncrossed 
         off number left.
4. If k is less than n then repeat 
         process from step (2).
5. Any number which has not been crossed off 
         is a prime number.

The Sieve of Eratosthenes

Lecture 3

16th - 18th Century Development of Mechanical Calculators

The adoption of the decimal system as a notation for numbers simplified the problem of describing quantities. This system, however, was not accompanied by corresponding advances in calculating techniques. From the 15th century onwards, a number of important areas gave rises to numerical calculations of great complexity. There was, however, little in the way of tools to help with such calculations. Three of the most important areas, in this respect, were:

In the former category we consider the work of 3 people: The technique of calculating via logarithms was described by Napier in the paper Mirifici logarithmorum canonis descriptio of 1614. Logarithms provide a mechanism for reducing multiplication and division to the (relatively) simple operations of addition and subtraction. A table of logarithms (to the base x) for some range of numbers (1 to 100, say) is a list which gives for each value, n, a quantity y called the logarithm of n to the base x (log^-x n). This quantity has the property that x^y = n. Thus if x=10, log^-10 1000 = 3. To perform multiplication of two numbers p and q, one finds logp and logq, adds these values, and then look up the anti-logarithm of the result. That this procedure is correct follows from the relationship

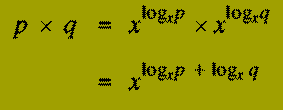
There are three problems with applying this approach:

The last drawback is acceptable, provided that the answers given are accurate enough for the application of interest. Napier described the technique of calculating with logarithms and provided some basic tables which addressed the first problem. The second difficulty was not easily dealt with by Napier's tables. The reason for this is that Napier did not understand the concept of base of a logarithm and his tables were constructed using the constant 1/e. e is a mathematical constant which has no simple physical definition: in differential calculus e may be defined as the unique constant such that the function e^x is its own derivative.

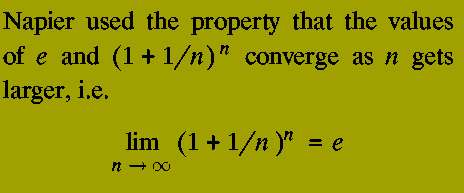
Napier, however, was not aware of this. The first practical tables of logarithms (in the sense that it was easy to construct the logarithms not in the table) were constructed by Napier's English contemporary Henry Briggs. Briggs discovered the idea of using 10 as the base. Now, if one has a table between 1 and a 100, and one wishes to find the log 1234 to the base 10, then one simply uses the fact that

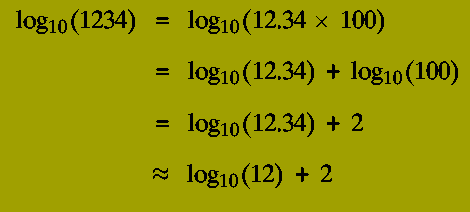
A mechanical analogue of logarithms was the slide rule invented by William Oughtred 1630.

Towards the end of his life, Napier invented a device which, for many years, was more highly regarded than his researches concerning logarithms: a mechanism for simplifying the task of multiplying numbers that has since become known as Napier's bones^9. Napier's bones were, in effect, a clever representation of multiplication tables:

The First Mechanical Calculators

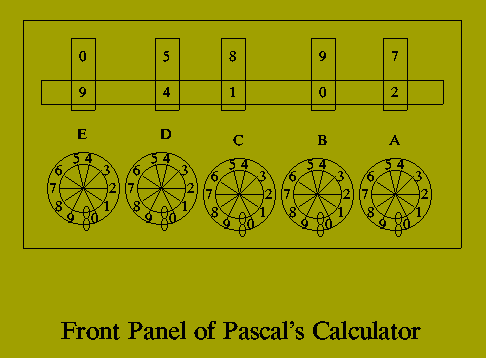
Between 1600 and 1700 a number of important mechanical calculating devices were designed and built. The most significant achievements in this area were the work of three people. Unfortunately, Schickard's device, known as the Calculating Clock, met with a problem: The construction of the first mechanical calculator had been attributed to the French mathematician, scientist and philosopher Blaise Pascal (1623-1662).

Gottfried Wilhelm von Leibniz em still noted today for his contributions to mathematics, logic, philosophy and calculation and the inventor of differential calculus in the form that it is known and used today, invented a calculator known as the Stepped Reckoner. This was an to build a machine that could not only add and subtract automatically but could also multiply and divide Leibniz solved the problem of multiplication by inventing a special type of gear, now called the Leibniz Wheel. Only one Stepped Reckoner is known to have been built. There are two reasons for this lack of development:

Lecture 4

19th Century Work Babbage, Hollerith, Boole

17th Century calculators demonstrated the feasibility of performing arithmetic operations by machines. They differed, however, from modern computers in a number of important ways.

In the course of the 19th century all but the last of these points were addressed in some way. The principal contributions in this period were those of:

Joseph-Marie Jacquard

Jacquard worked in the textile industry in France. Production of patterned cloth during the 18th century was a time-consuming and highly skilled task. Jacquard devised a mechanism em the Jacquard Loom em by which complex patterns could be woven automatically. To record a pattern and control the operation of a loom, a

Program of punched cards

was employed. This is the earliest example of using punched card mechanisms to control a complex process. One program, of 10,000 cards was used to produce a black-and-white silk portrait of Jacquard. The technique of using punched cards as a control mechanism was subsequently taken up by developers of later calculators.

Hollerith's Census Collator

One of the oldest statistical collection tasks is that of

Census Taking

A number of ancient records give accounts of census activities, e.g.

2 Samuel 2:1-9

Luke 2:2

In Roman society the office of Censor was an important public position. Census statistics were used to determine

Article 1, Section 3 of the U.S. Constitution requires that a Population Census be held every 10 years in the U.S. The first of these was held in August 1790. Information took 9 months to gather and process for a population of about 4 million. By 1860 the population of the U.S. had increased to over 31 million. Processing census data was so time-consuming that there was a danger of the previous census still being collated when the constitutional requirement to hold the next one arose. Hollerith became interested in the problem following the 1880 Census. While working for the Census Office he met John Shaw Billings who was responsible for analysing the returns. Together they thought of the idea of carrying out the processing automatically. Although Hollerith's company subsequently lost a Patent Suit in the Supreme Court which removed his sole rights to the technology, his ideas had considerable influence.

Charles Babbage and Ada Lovelace

In the 1820s the British Admiralty Office was using tables of logarithms, trigonometric functions, and astronomical data, parts of which had been compiled almost 200 years earlier. Such tables were essential for validating scientific experiments and hypotheses. Through errors in calculation and transcription these tables were riddled with errors. Corrigenda ran to 7 volumes. The corrigenda themselves were full of errors. Charles Babbage became involved with building calculating machines while checking these tables. Babbage's idea was to build a machine that could calculate and print these tables automatically. This would (if the machine worked correctly) eliminate any possibility of transcription errors. In 1822, Babbage presented a paper to the Royal Astronomical Society, describing how a mathematical technique em The Method of Differences, which allowed the computation of intricate functions to be reduced to repeated additions em could be used as the basis of a scientific table calculator. Babbage demonstrated a simple machine that could calculate tables of squares and cubes. The Society supported Babbage's proposal to build a machine that worked to an accuracy of 20 decimal places. The proposed machine was called the

Difference Engine

The Exchequer gave a grant of po1500 towards its construction. Babbage estimated that about po5000 and 2-3 years work would be needed on it. Babbage worked on the machine for 10 years, spending po34,000. The Difference Engine was never completed. Its remains are currently in the Science Museum, London. There are a number of reasons why Babbage ceased work on the Difference Engine, but the principal one is that he had conceived the idea of a far more ambitious machine:

The Analytic Engine

This machine would have rendered the Difference Engine obsolete. The design and operation that Babbage envisaged for this machine comprised many of the ideas underlying modern digital electronic computers. The Analytic Engine would consist of two parts: Babbage's description of the Analytic Engine

The whole process of the machine was to be controlled by punched-cards: certain of which would contain the data and others which would describe the operations (program) to be carried out. In terms of modern machines, Babbage's Analytic Engine, proposes the fundamental components of

One these grounds Babbage has a strong claim to be regarded as the inventor of (even though not the first to build) the modern computer. Many of the ideas concerning program construction and the design of the Analytic Engine were the work of Babbage's collaborator Augusta Ada Byron, Countess of Lovelace. Ada Lovelace was the only (legitimate) daughter of the English poet Lord George Byron, who had died when she was 14. She was a gifted mathematician and had become interested in Babbage's work on encountering an early prototype of the Difference Engine. She was one of the few people at the time who realised the significance of Babbage's work. All of the surviving accounts of the Analytic Engine and its working are from her descriptions. Ada Lovelace is generally acknowledged to be the first writer of `computer programs'. The language ADA is named after her. The Analytic Engine was never built (or even close to being built). Babbage died in 1871, and at the end of his life was treated with ridicule: this was largely on account of his extreme dislike of street musicians and children. Both groups would perform outside his home with the sole object of annoying him.

George Boole

The 19th Century figure whose work would turn out to be of greatest significance in the development of modern computers was the English self-taught mathematician George Boole. Boole developed the algebraic system, now named Boolean algebra, which is used for expressing and evaluating logical propositions and arguments. As a result of his formalism it became possible to express arithmetic and other functions in terms of operations on binary (0 or 1) values. Moving to the binary representation of information meant that mechanical gearing systems could be replaced by conceptually far simpler methods. The realisation that data could be manipulated in binary was probably the single most significant stage in the development of modern computer systems.

Lecture 5

The First Digital Electronic Computers 1934-1955

Although Babbage's plans for the Analytic Engine anticipated the design of modern computers, they were unrealisable since Babbage was still using mechanical gears as a computational analogue. The engineering facilities of the time were not capable of building components of the precision and complexity required.

Babbage had aimed to build a machine which could:

The main technological insight that made modern computer systems possible was that

binary switching components

could be used to represent information and afford a means of manipulating such representations.

Using electrically driven switches we can

Using binary as the basic representation means that: All modern computing systems can, at the most basic level of operations, be described in terms of complex networks of binary switching components. The first such `switching components' were electro-mechanical relay-contact switches. These comprised two metal contacts connected by a hinge; on receipt of a sufficiently high voltage the two metal contact closed together to allow a current to pass through them. Almost all subsequent improvements in computer design (speed and reliability) have come about through the invention of better (smaller, faster, more reliable) switching components: valves, transistors, LSI chips, VLSI chips.

Development of First Electrical Machines

in Germany (1936-44) Konrad Zuse and Helmut Schreyer

Konrad Zuse (1910-) was a German electrical engineer who became interested in designing automatic computers while a student in Berlin. Zuse initially wished to build a machine to solve systems of simultaneous linear equations, e.g. 


3x + 2y + 3z  =  18
5x + 3y + 2z  =  17
4x + 6y + 7z  =  37

where one is required to find (usually, unique) values for the k variables which simultaneously satisfy the k identities. In the example, the (unique) solution is x=1, y=2, and z=3. Such systems commonly arise in engineering applications as a model for representing trade-offs between different criteria in building structures, e.g. weight, strength, rigidity etc of materials used. Although not mathematically difficult to solve considerable amounts of calculation are involved. The traditional approach (known as Gaussian elimination) becomes extremely laborious when more then four identities are to be dealt with. In engineering applications such as architecture systems involving several hundred equations often arose and constructing feasible solutions to such systems would require months of work by a number of teams. Zuse had the idea of carrying out the required calculations by a machine while he was a student in 1934. Zuse recognised that such a machine would need to meet three basic criteria.

In 1936, while working at the Henschel Aircraft Company in Berlin, Zuse started to build his first machine: the Z1. This was undertaken entirely privately at his own expense. This was completed in 1938, however, the arithmetic unit did not function correctly. Zuse was still using a basically mechanical system. With his second machine, the Z2, in which Zuse dispensed with the mechanical plates of his prototype machine (except for the memory design which had worked successfully in the Z1) and substituted electromechanical relays instead. This had two effects: The suggestion that electro-mechanical relay switches be used had come from Zuse's colleague, Helmut Schreyer, an electrical engineer. Schreyer had actually proposed using a purely electronic device called a thermionic valve (similar to the valves found in old wireless sets). This could be used both as a memory device and as a switching mechanism. Schreyer's idea was eventually taken up in the early 1950s by prototype British and U.S. computers. The final version of the Z2 was completed in 1939. Zuse was conscripted at the outbreak of the Second World War eventually ending up working at the Aerodynamics Research Institute. Schreyer, who was not conscripted, continued on his own idea of building a machine using purely electronic components, in this case thermionic valve. In 1942, Schreyer submitted a research proposal describing his machine and its potential to the German High Command: it was rejected as being of no importance. Zuse was only able to work on his next machine, the Z3, by presenting it as a special-purpose calculator for aircraft design. The Z3, which was the first ever working general-purpose programmable computer was completed in December 1941.

The machine which comprised a tape reader, operators console and functional units containing about two and a half thousand relays was built for very little cost, about po1000 Zuse went on to built a larger machine, the Z4, which after being relocated a number of times during its construction to avoid bombing attacks, was completed in the late 1940s. It was subsequently placed in a technical institute in Zurich in 1950 were for a number of years it was the only available powerful calculating tool in mainland Europe. The Z3 was destroyed by an air-raid on Berlin in April 1945.

Computers in the U.S. of A.

Aiken, Atanasoff, Eckert, Mauchley and von Neumann 1937-1955 The history of electronic computer development in the U.S. is extremely involved and (still) the subject of some controversy. Most of this is caused by the roles of three of the participants in the development: The last two were at the centre of a Patents Dispute (under which they claimed to have `invented' the first modern electronic computer). In one form or another this dispute occupied various U.S. Courts from 1952 until October 19th 1973. It ended when the Supreme Court ruled against Eckert and Mauchly's claim. In fact, historically, Eckert and Mauchly's assertion to be the inventors of the electronic computer has little to justify it. The work of Zuse and Schreyer predates their efforts by at least 5 years. It is also the case that British work in the 1940s has at least as strong a claim as Eckert and Mauchly's. Zuse's work was unknown in the U.S until much later. British work was classified and details of it were only available from 1975. The first U.S. figure to deal with digital electronic computers was Howard Aiken. Aiken in 1937 at Harvard proposed a structure for what he regarded as an `ideal' computer. This combined elements of Babbage's ideas together with Hollerith's punched card techniques. Aiken's proposals attracted support from I.B.M. His machine, the Mark 1, was built between 1939 and 1944. It used electro-mechanical relays, contained 3/4 million components, and could complete a month's manual calculation in a single day. John Atanasoff and his collaborator Clifford Berry produced a design for a valve-based computer. Atanasoff constructed a simple electronic calculator and set about building a full-scale computer. Only sections of this were completed though. The Atanasoff-Berry Computer (ABC) was rediscovered in the 1960s. Despite the fact that it was never built, this discovery played an important r&ole in the subsequent Patent judgement against Eckert and Mauchly.

Eckert and Mauchly

Mauchly, as with Shreyer and Atanasoff, was interested in employed valves as a switching component for electronic computers. His primary interest was in weather forecasting and the possibility of carrying this out by a machine. Eckert and Mauchly met at the Moore School in Pennsylvania and in May 1943 persuaded the U.S. Government to fund the construction of a digital computer. The final machine, called ENIAC, was completed in May 1944. It was extemely large (3000 cubic feet, 30 tons weight, 100,000 components); and very fast being able to multiply in 3 milliseconds. Eckert and Mauchly went on to found their own company.

John von Neumann

von Neumann was involved in the design of the successor to ENIAC, EDVAC, which made a number of technical improvements upon ENIAC. He is, mistakenly, credited as the inventor of the digital electronic computer. von Neumann is mainly important for two achievements

Developments in the U.K.

COLOSSUS to EDSAC

In 1938, the British Intelligence Service obtained a complete description of the German cipher machine ENIGMA. This was used to communicatew field orders by the German Military High Command. Possession of the machine was not sufficient, in itself, to decipher intercepted communications, since the machine encoded using a code sequence that was changed daily. Knowledge of the machine's operation, however, enabled the number of possible keys available at a particular time to be greatly reduced. The initial British attempts to build a (special-purpose) digital computer took place at Bletchely Park under the direction of Alan Turing. The aim of the research em codenamed Project ULTRA em was to build a machine that could identify the codewords used to configure ENIGMA. The final machine em called COLOSSUS em was started in January 1943 and completed in December 1943. A succesor, the Mark II, had been built by December 1944. This research and its results were not made public until 1975, under the 30 Year Rule governing the release of classified material. After the end of World War 2, British engineers made use of U.S. work and a number of succesful systems were built:

Lecture 6

Making Computing Easier

The Development of High-Level Programming Languages 1955-1970

Using a computer system in the early 1950s would often be an extremely frustrating experience. There were two causes of this:

The technological problem was caused by the use of valves:

For the earliest machines, hours could be spent in setting up a series of calculations, only to for the machine to have a valve failure (losing all the data) when the program was run. Although dealing with heating continues to be a problem for computer systems the reliability of basic switching components greatly improved after the invention of the transistor in 1947. The TRADIC, built in 1954, was the first transistor-based computer. Developments in semiconductor techniques and device physics eventually led to the appearance of VLSI chips in the mid-1970s. On these, a computer processor of far greater power than the 1940s machines could be placed in a space the area of a fingernail. The first machines typically occupied the space of several gymnasia. The problem of making computer systems more accessible, however, was a far less tractable one. John von Neumann, in his description of computer organisation, had shown how operations and data could be encoded in binary using a single word of the computer memory. The processor would then decode the binary instructions and execute the specified command. For the first computer systems, a complete program of binary instructions would have to be fed into the machine by hand. Even for quite simple programs this might necessitate entering several thousand 0s and 1s. A single error would render the program useless. Maurice Wilkes' invention of assembly language, whereby simple mnemonics where used for program instructions (ADD, STORE, LOAD) helped a little in avoiding such transcription errors. Such programs were still difficult to write and still had to be translated (by hand) into a form that could be entered into a computer. High-level programming languages were developed to allow programs to be described in more natural way. A single statement in a high-level language would correspond to several machine instructions. A special program, called a compiler, was used to translate such programs into a form that a computer could run. In this lecture we examine the first languages developed and their specific areas of application.

FORTRAN

(FORmula TRANslation) Readability and efficiency were important considerations in the design of FORTRAN.

COBOL

(COmmon Business Oriented Language) e.g. A = B+C in FORTRAN become

ADD B TO C GIVING A

in COBOL. Despite its attempts to mimic natural language, writing COBOL programs was as difficult as writing in any other programming language. This led to the realisation that the difficulty with programming computers is not in describing the details of the program but in constructing the algorithm which the program will encode.

LISP

(LISt Processing Language)

ALGOL60 and ALGOL68

(ALGOrithmic Language)

PED Home Page