The traditional description logics can be used for representing common
and individual knowledge about the world (domain of application). Recently
description logics have been extended to allow the representation
of the knowledge and the beliefs of multiple agents in one knowledge
base [3,11]. In MOTEL we formulate knowledge and belief as additional modal operators.
We are using 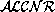 [1] as a base
language.
That is,
we assume three disjoint alphabets,
the set of concept names C,
the set of role names R, and
the set of individual objects O.
The set of concept terms (or just concepts) and
role terms (or just roles) is inductively defined as
follows. Every concept name is a concept term and every role
name is a role term. Now assume that C, D are concepts,
and R, S are roles. Then
and([C,D]), not(C), some(R,C),
atleast(n,R), atmost(n,R)
are concept terms, and
and([R,S]), inverse(R), restrict(R,C) are role terms.
The sentences of
[1] as a base
language.
That is,
we assume three disjoint alphabets,
the set of concept names C,
the set of role names R, and
the set of individual objects O.
The set of concept terms (or just concepts) and
role terms (or just roles) is inductively defined as
follows. Every concept name is a concept term and every role
name is a role term. Now assume that C, D are concepts,
and R, S are roles. Then
and([C,D]), not(C), some(R,C),
atleast(n,R), atmost(n,R)
are concept terms, and
and([R,S]), inverse(R), restrict(R,C) are role terms.
The sentences of 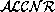 are divided into terminological sentences and
assertional sentences.
If C and D are concepts and R and S are roles then
defprimconcept(C,D) and
defprimrole(R,S) are terminological
sentences.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(a,C) and assert_ind(a,b,R)
are assertional sentences.
As in [1] we do not allow terminological cycles.
are divided into terminological sentences and
assertional sentences.
If C and D are concepts and R and S are roles then
defprimconcept(C,D) and
defprimrole(R,S) are terminological
sentences.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(a,C) and assert_ind(a,b,R)
are assertional sentences.
As in [1] we do not allow terminological cycles.
For the extended language Mod-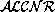 we assume in addition that
we have an alphabet
M of modal operator names. Also, there is a distinguished
subset A of the individual objects, called the set of
agents.
We have a distinguished concept name ` all' denoting
the set of all agents with which we express mutual belief.
The set of concepts and the set of roles of Mod-
we assume in addition that
we have an alphabet
M of modal operator names. Also, there is a distinguished
subset A of the individual objects, called the set of
agents.
We have a distinguished concept name ` all' denoting
the set of all agents with which we express mutual belief.
The set of concepts and the set of roles of Mod-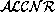 contains
all the concepts and roles of its sublanguage
contains
all the concepts and roles of its sublanguage 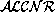 and in
addition it contains the
concepts b(m,a,C), d(m,a,C), bc(m,C,D), and
dc(m,C,D). A modal context is a list of modal operators
of the form b(m,a), d(m,a), bc(m,C), and
dc(m,C). If L is a modal context,
C and D are concepts and R and S are roles then
defprimconcept(L,C,D) and
defprimrole(L,R,S) are terminological
sentences in Mod-
and in
addition it contains the
concepts b(m,a,C), d(m,a,C), bc(m,C,D), and
dc(m,C,D). A modal context is a list of modal operators
of the form b(m,a), d(m,a), bc(m,C), and
dc(m,C). If L is a modal context,
C and D are concepts and R and S are roles then
defprimconcept(L,C,D) and
defprimrole(L,R,S) are terminological
sentences in Mod-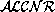 .
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(L,a,C) and assert_ind(L,a,b,R)
are assertional sentences in Mod-
.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(L,a,C) and assert_ind(L,a,b,R)
are assertional sentences in Mod-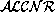 .
.
We use a translational approach to provide the usual inference
mechanisms, i.e. solving the
consistency, the subsumption, the instantiation and the realization
problem. Obviously, 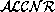 knowledge
bases can be translated into first-order logic
theories. There are also well-known relational translation methods for modal
logics. In [8] (also available as
we have developed an improved
translation method for Mod-
knowledge
bases can be translated into first-order logic
theories. There are also well-known relational translation methods for modal
logics. In [8] (also available as
we have developed an improved
translation method for Mod-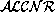 which provides an elegant translation of knowledge bases into first-order logic theories. In a
prototypical implementation, the MOTEL system,
we use a Prolog-based system with loop-checking as inference machine.
which provides an elegant translation of knowledge bases into first-order logic theories. In a
prototypical implementation, the MOTEL system,
we use a Prolog-based system with loop-checking as inference machine.


Next: Quantitative Information
Up: The MOTEL Knowledge Representation System
Previous: A Description Logic for NLP
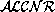 [1] as a base
language.
That is,
we assume three disjoint alphabets,
the set of concept names C,
the set of role names R, and
the set of individual objects O.
The set of concept terms (or just concepts) and
role terms (or just roles) is inductively defined as
follows. Every concept name is a concept term and every role
name is a role term. Now assume that C, D are concepts,
and R, S are roles. Then
and([C,D]), not(C), some(R,C),
atleast(n,R), atmost(n,R)
are concept terms, and
and([R,S]), inverse(R), restrict(R,C) are role terms.
The sentences of
[1] as a base
language.
That is,
we assume three disjoint alphabets,
the set of concept names C,
the set of role names R, and
the set of individual objects O.
The set of concept terms (or just concepts) and
role terms (or just roles) is inductively defined as
follows. Every concept name is a concept term and every role
name is a role term. Now assume that C, D are concepts,
and R, S are roles. Then
and([C,D]), not(C), some(R,C),
atleast(n,R), atmost(n,R)
are concept terms, and
and([R,S]), inverse(R), restrict(R,C) are role terms.
The sentences of 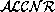 are divided into terminological sentences and
assertional sentences.
If C and D are concepts and R and S are roles then
defprimconcept(C,D) and
defprimrole(R,S) are terminological
sentences.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(a,C) and assert_ind(a,b,R)
are assertional sentences.
As in [1] we do not allow terminological cycles.
are divided into terminological sentences and
assertional sentences.
If C and D are concepts and R and S are roles then
defprimconcept(C,D) and
defprimrole(R,S) are terminological
sentences.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(a,C) and assert_ind(a,b,R)
are assertional sentences.
As in [1] we do not allow terminological cycles.
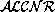 we assume in addition that
we have an alphabet
M of modal operator names. Also, there is a distinguished
subset A of the individual objects, called the set of
agents.
We have a distinguished concept name ` all' denoting
the set of all agents with which we express mutual belief.
The set of concepts and the set of roles of Mod-
we assume in addition that
we have an alphabet
M of modal operator names. Also, there is a distinguished
subset A of the individual objects, called the set of
agents.
We have a distinguished concept name ` all' denoting
the set of all agents with which we express mutual belief.
The set of concepts and the set of roles of Mod-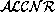 contains
all the concepts and roles of its sublanguage
contains
all the concepts and roles of its sublanguage 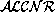 and in
addition it contains the
concepts b(m,a,C), d(m,a,C), bc(m,C,D), and
dc(m,C,D). A modal context is a list of modal operators
of the form b(m,a), d(m,a), bc(m,C), and
dc(m,C). If L is a modal context,
C and D are concepts and R and S are roles then
defprimconcept(L,C,D) and
defprimrole(L,R,S) are terminological
sentences in Mod-
and in
addition it contains the
concepts b(m,a,C), d(m,a,C), bc(m,C,D), and
dc(m,C,D). A modal context is a list of modal operators
of the form b(m,a), d(m,a), bc(m,C), and
dc(m,C). If L is a modal context,
C and D are concepts and R and S are roles then
defprimconcept(L,C,D) and
defprimrole(L,R,S) are terminological
sentences in Mod-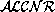 .
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(L,a,C) and assert_ind(L,a,b,R)
are assertional sentences in Mod-
.
If C is a concept, R is a role, and a, b are
individual objects
then assert_ind(L,a,C) and assert_ind(L,a,b,R)
are assertional sentences in Mod-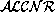 .
.
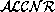 knowledge
bases can be translated into first-order logic
theories. There are also well-known relational translation methods for modal
logics. In [
knowledge
bases can be translated into first-order logic
theories. There are also well-known relational translation methods for modal
logics. In [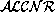 which provides an elegant translation of knowledge bases into first-order logic theories. In a
prototypical implementation, the MOTEL system,
we use a Prolog-based system with loop-checking as inference machine.
which provides an elegant translation of knowledge bases into first-order logic theories. In a
prototypical implementation, the MOTEL system,
we use a Prolog-based system with loop-checking as inference machine.