A random generators for modal formulae

There are five parameters: the number of propositional variables N, the number of modalities M, the number of modal subformulae per disjunction K, the number of modal subformulae per conjunction L, the modal degree D, and the probability P. Based on a given choice of parameters random modal KCNF formulae are defined inductively as follows.

A random (modal) atom of degree 0 is a variable randomly chosen from the set of N propositional variables.
A random modal atom of degree D, D{>}0, is with probability P a random modal atom of degree 0 or an expression of the form [i] F, otherwise, where [i] is a modality randomly chosen form the set of M modalities and F is a random modal KCNF clause of modal degree D-1 (defined below).
A random modal literal (of degree D) is with probability 0.5 a random modal atom (of degree D) or its negation, otherwise.
A random modal KCNF clause of degree D) is a disjunction of K random modal literals (of degree D).
Now, a random modal KCNF formula (of degree D) is a conjunction of L random modal KCNF clauses (of degree D).

The parameter settings considered in Giunchiglia and Sebastiani (1996b) are the following.

	N	M	K	D	P		N	M	K	D	P
PS0	5	1	3	2	0.5	PS5	4	1	3	2	0.5
PS1	3	1	3	5	0.5	PS6	4	2	3	2	0.5
PS2	3	1	3	4	0.5	PS7	4	5	3	2	0.5
PS3	3	1	3	3	0.5	PS8	4	10	3	2	0.5
PS4	3	1	3	2	0.5	PS9	4	20	3	2	0.5

It is important to note that for D=0 and K=3 random modal KCNF formulae do not coincide with random 3SAT formulae (as mistakenly claimed by Giunchiglia and Sebastiani (1996b)). Generating a clause of a random 3SAT formula means randomly generating a set of three propositional variables and then negating each member of the set with probability 0.5. In contrast, generating a random modal 3CNF clause of degree 0 means randomly generating a multiset of three propositional variables and negate each member of the multiset with probability 0.5. For example, (p | q | -r) is a 3SAT clause and also a modal 3CNF clause of degree 0. The clauses (p | -p | p) and (p | p | q) are not 3SAT clauses, but both are random modal 3CNF clauses of degree 0. In random modal 3CNF formulae of higher degree, such clauses occur within the scope of a modal operator. For example, contradictory expressions like -[1](p | -p | p) may occur. Thus, random modal KCNF formulae contain tautological and contradictory subformulae.

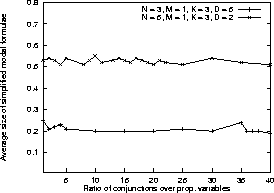
Occurrences of tautological and contradictory subformulae in the randomly generated formulae are not a problem in themselves as long as the evalution of the methods takes this fact into accout. Let us first investigate the question whether the occurrence of tautological and contradictory subformulae is only a rare phenomenon or whether it could seriously influence the evalution. To this end we apply standard simplication rules to the randomly generated formulae to remove tautological and contradictory subformulae and compare the size of the formulae before and after the simplification. The following graph shows the effect on the average formula size for two of the parameter settings used by Giunchiglia and Sebastiani (1996b).

Figure 1: The effect of simplification

For the random modal 3CNF formulae generated using three propositional variables, on average, the size of a simplified formula is only 1/4 of the size of the original formula. For the second parameter setting we observe a reduction to 1/2 of the original size. In other words, one half to three quarters of the random modal 3CNF formulae is ``logical garbage'' that can be eliminated at little cost.

Thus, occurrences of tautological and contradictory subformulae are not a rare phenomenon for the parameter settings used by Giunchigila and Sebastiani (1996b). Any modal theorem prover which does not efficiently eliminiate such trivial subformulae will have a disadvantage on these random modal formulae.