Trival satisfiable and trivial unsatisfiable formulae
We have just seen that a major cause of the difference in
computational behaviour of KsatLISP and KRIS is the absence
of the preprocessing step in KRIS. To explain the remaining
difference we study the quality of the random modal 3CNF
formulae. Suppose that we want to test a random modal 3CNF formula
with N propositional variables for
satisfiability in a Kripke model with only one world. We have
to test at most 2^N truth assignments to the propositional
variables. Since N <= 5 for the modal formulae under
consideration, this is a trivial task, even by the truth
table method. We say a random modal 3CNF formula F is
trivially satisfiable if F is satisfiable in a Kripke model
with only one world. We also say a random modal 3CNF
formula F is trivially unsatisfiable if the conjunction
of the purely propositional clauses of F is
unsatisfiable. Again, testing whether F is trivially unsatisfiable
requires only the consideration of 2^N truth assignments.
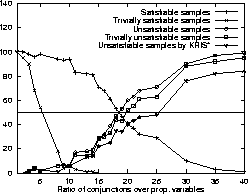
The following graphs show the percentage of satisfiable,
trivially satisfiable, unsatisfiable, trivially unsatisfiable, and
unsatisfiable formulae in the samples detected by KRIS* of the set of
test formulae generated for PS0.
Figure 3: Percentage of trivial problems for PS0
|
We see that almost all unsatisfiable test formulae are
trivially unsatisfiable. This holds also
for all the other parameter settings used by Giunchiglia and
Sebastiani. This indicates, none of the parameter settings is suited
to generate challenging unsatisfiable modal formulae.
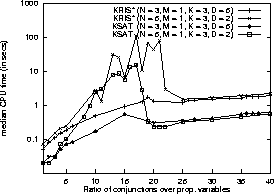
Figure 4: Median CPU time performance of KsatLISP and KRIS*
|
If we consider the graphs in Figures 3 and 4 together,
we observe the graph of KRIS* (in Figure 4) deviates
a lot (by a factor of more than 100) from the graph of KsatLISP
for ratios L/N between 19 and 21. This
is the area near the crossover point where the percentage of trivially
unsatisfiable formulae rises above 50%, however, the percentage of
unsatisfiable formulae detected by KRIS* is still below 50% in this
area, that is, KRIS* does not even detect all trivially unsatisfiable
formulae within the time-limit.
This phenomenon is linked to the `heuristics' used by KRIS* to select the
disjunctions to which it applies the disjunction rule: It simply selects
the disjunctions in reverse order in which they appear in the input.
As far as the random formulae are considered, the purely
propositional disjunctions which cause the unsatisfiability of a trivially
unsatisfiable formula might be far apart from each other in the input.
Consequently, KRIS* applies the disjunction elimination rule not only to these
propositional disjunction, but also to other disjunctions, introducing
irrelevant branches into the search space. Backtracking through all these branches
might not be completed within the time-limit.
There are several solutions to this problem. First, we could KRIS* with a better
heuristics, for example the one used in KsatLISP. Second, we could implement a more
intelligent backtracking than the chronological backtracking used in KRIS*. We will
not investigate these solutions any further. On the following
page we will see that rearranging the disjunction in the
input of KRIS* already provides a significant improvement of its performance.
Top: Contents |
Previous: KSAT versus KRIS: Simplification |
Next: KSAT versus KRIS: The effect of sorting


