


Next: Problem and Procedure
Up: Invariant Serach via Temporal
Previous: Invariant Serach via Temporal
First-order temporal logic over natural numbers is a very expressive formalism,
allowing specification at natural level of abstraction, of
various computational phenomena, algorithms and protocols.
However, the reasoning in FOLTL is very complex.
The logic itself, and even very small
fragments, are non-recursively axiomatizable. That is why developing
the proof methods, possibly based on heuristics, for fragments of FOLTL
is the important task.
The key part of the reasoning in FOLTL is essentially inductive.
For example, the following inductive
proof rule can be used to prove 'always' conclusions.
From
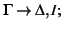
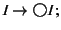
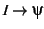 derive
derive
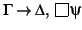 However, the finding the
invariant formula
However, the finding the
invariant formula 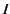 during the proof search is a complex task and, in
general, there is no complete procedure to achieve this.
In the paper [BDFL02] a method of finding the
invariants in a class of first-order monodic [HWZ00]
temporal
formulae has been described and
its completeness has been established.
The method is based on a clausal temporal resolution technique
[Fis91,FDP01].
Here we decribe an algorithm, based on this method, but extended to
wider class of formulae, where it serves as, in general, incomplete,
but useful procedure for the proving 'always'-formulae
(i.e. of the form
during the proof search is a complex task and, in
general, there is no complete procedure to achieve this.
In the paper [BDFL02] a method of finding the
invariants in a class of first-order monodic [HWZ00]
temporal
formulae has been described and
its completeness has been established.
The method is based on a clausal temporal resolution technique
[Fis91,FDP01].
Here we decribe an algorithm, based on this method, but extended to
wider class of formulae, where it serves as, in general, incomplete,
but useful procedure for the proving 'always'-formulae
(i.e. of the form 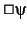 ).
This algorithm has been implemented in the higher-order logic programming language
).
This algorithm has been implemented in the higher-order logic programming language
 [Lpro] with the general control provided
by the proof planning system
[Lpro] with the general control provided
by the proof planning system 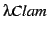 [RSG98]. We here
outline this implementation and
discuss some of its features.
[RSG98]. We here
outline this implementation and
discuss some of its features.



Next: Problem and Procedure
Up: Invariant Serach via Temporal
Previous: Invariant Serach via Temporal
Alexei Lisitsa
2003-06-13