Note that where a top down approach is used to identify a detailed design this is referred to as top down design. Where the technique is used to identify program statements this is referred to as step wise refinement. The latter was first proposed by Niklaus Wirth (the inventor of the imperative programming language PASCAL) in the early 1970's (Wirth 1971). The disadvantages of using a top down approach for detailed design, or the identification of individual implementation statements, may be listed as follows:
There is no precise definition as to what constitutes an "easily solvable sub-problem". To a degree this is of course dependent on the experience and background of the designer/programmer. However, a useful guideline is that:
This only gets us part of the way because we now need to have some idea as to the type of problems that can be addressed by a single procedure or function. Again there are no definite rules here, but we should take note of the following guidelines:
Often, to identify a procedure sized problem, it is necessary to go one level further in the top-down analysis. There is nothing wrong with this.
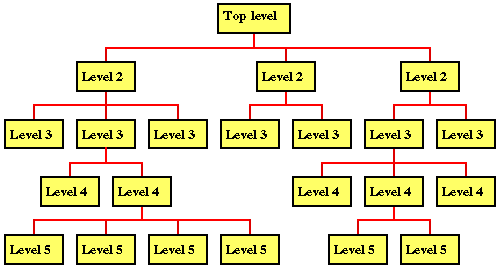
The simplest method of describing a top-down analysis is to use a tree structure such as that shown below. In such a structure each branch in the tree originates at a node. The top most node (i.e. the first or top level in the analysis) is sometimes referred to as the root node, and the bottom most nodes are sometimes referred to as the leaf nodes. Each node represents an abstraction in the problem's decomposition with the leaf nodes representing the lowest level of abstraction. There can only be one root node (the highest level of abstraction).

We also talk of nodes as being parents, children or siblings of other nodes:
With respect to tree structures used to represent top-down problem analysis the following should be noted:
Given a particularly complicated problem it may be appropriate to describe the analysis using a number of tree structures using connectors to indicate where parts of the overall tree structure "meet up".
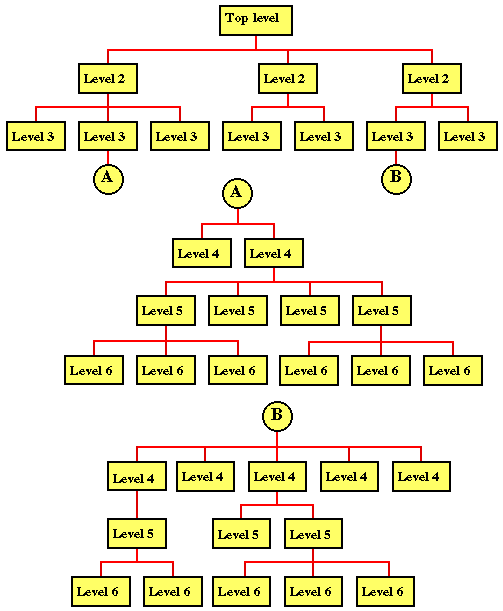
There is nothing wrong with doing a number of top-down analyses, where each new break down is a more refined version of the previous analysis. A typical situation where we might wish to redefine our hierarchy is where we discover that some component of a problem's decomposition appears more than once (i.e. in separate branches) in the tree. In this case we should move the component higher up the tree so that it becomes a parent node of all the sub-problem nodes where it is required (although we cannot move a node so far up the tree that it becomes a second root node). The reason for this is that the top down break down should also reflect:
Note: a problem may be so large that, to become manageable, its solution may require several programs. For example each of the level 2 components in a top down decomposition might be addressed by individual programs with one acting as the "main" program (more on this later).
Design and create an Ada program that, given a temperature in Centigrade converts it to Fahrenheit and vice-versa. Output should be accurate to one decimal place. To convert from Centigrade to Fahrenheit the following identity is appropriate:
F = (9/5 x C) + 32
To convert from Fahrenheit to Centigrade we will use:
C = (F - 32) x 5/9
Note also that we have written a similar program to convert Centigrade temperatures to Fahrenheit. We can reuse this code (code reuse is an important economic issue in software engineering).
A top-down analysis of the proposed problem is given below.
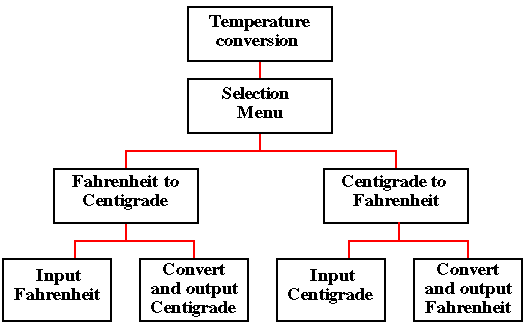
With respect to the above we can identify three procedures:
| NAME | DESCRIPTION | TYPE | RANGE |
|---|---|---|---|
| MENU_ITEM | Global input variable | CHARACTER | Default |
| NAME | DESCRIPTION | TYPE | RANGE | |||
|---|---|---|---|---|---|---|
| CENT_TEMP | Local input variable | CENTIGRADE | -50.0..100.0 TEMPERATURE | Local output variable | FLOAT | Default |
| NAME | DESCRIPTION | TYPE | RANGE | |||
|---|---|---|---|---|---|---|
| FAHR_TEMP | Local input variable | FAHRENHEIT | -58.0..212.0 TEMPERATURE | Local output variable | FLOAT | Default |
The above includes the programmer defined types CENTIGRADE and FAHRENHEIT which will be expressed as subtypes of the type FLOAT. A complete Nassi-Schneiderman design for the above is given below, followed by a flow chart.


Commence the implementation at the top-level of the analysis using stubs for lower level procedures:
-- TEMPERATURE CONVERSION
-- 15 August 1997
-- Frans Coenen
-- Dept Computer Science, University of Liverpool
with TEXT_IO;
use TEXT_IO;
procedure TEMP_CONVERT is
package FLOAT_INOUT is new FLOAT_IO(FLOAT);
use FLOAT_INOUT;
MENU_ITEM: CHARACTER;
------------------------------------------------------------
-- CENTIGRADE TO FAHRENHEIT CONVERSION
procedure CENT_2_FAHR is
begin
PUT_LINE("CENT_2_FAHR procedure");
end CENT_2_FAHR;
------------------------------------------------------------
-- FAHRENHEIT TO CENTIGRADE CONVERSION
procedure FAHR_2_CENT is
begin
PUT_LINE("FAHR_2_CENT procedure");
end FAHR_2_CENT;
------------------------------------------------------------
-- TOP LEVEL
begin
-- Output Menu
PUT_LINE("MENU OPTIONS");
PUT_LINE("C - Centigrade to Fahrenheit conversion");
PUT_LINE("F - Fahrenheit to Centigrade conversion");
GET(MENU_ITEM);
-- Check menu input
if (MENU_ITEM = 'C' OR MENU_ITEM = 'c') then
CENT_2_FAHR;
else
if (MENU_ITEM = 'F' OR MENU_ITEM = 'f') then
FAHR_2_CENT;
else
PUT("Invalid menu selection: ");
PUT(MENU_ITEM);
NEW_LINE;
end if;
end if;
end TEMP_CONVERT;
Notes:
-- Check menu input
if (MENU_ITEM = 'C' OR MENU_ITEM = 'c') then
CENT_2_FAHR;
elsif (MENU_ITEM = 'F' OR MENU_ITEM = 'f') then
FAHR_2_CENT;
else
PUT("Invalid menu selection: ");
PUT(MENU_ITEM);
NEW_LINE;
end if;
On completion of this top level implementation we should test its operation. In this case we should run test cases for each of the possible menu inputs including an invalid input. A suitable set of test cases is given in the table below.
| TEST CASE | EXPECTED RESULT |
|---|---|
| MENU_ITEM | Output |
| C | CENT_2_FAHR procedure |
| c | CENT_2_FAHR procedure |
| F | FAHR_2_CENT procedure |
| f | FAHR_2_CENT procedure |
| M | Invalid menu selection: M |
Once testing of this level is complete we can go on to implement the following level:
-- TEMPERATURE CONVERSION
-- 15 August 1997
-- Frans Coenen
-- Dept Computer Science, University of Liverpool
with TEXT_IO;
use TEXT_IO;
procedure TEMP_CONVERT is
package FLOAT_INOUT is new FLOAT_IO(FLOAT);
use FLOAT_INOUT;
MENU_ITEM: CHARACTER;
------------------------------------------------------------
-- CENTIGRADE TO FAHRENHEIT CONVERSION
procedure CENT_2_FAHR is
subtype CENTIGRADE is FLOAT range -50.0..100.0;
CENT_TEMP : CENTIGRADE;
TEMPERATURE : FLOAT;
begin
-- Input Centigrade value
PUT_LINE("Input temperature in degrees Centigrade (float): ");
GET(CENT_TEMP);
-- Conversion
TEMPERATURE := CENT_TEMP * (9.0/5.0) + 32.0;
-- Output Fahrenheit value
PUT("The equivalent in degrees Fahrenheit is: ");
PUT(TEMPERATURE, FORE=>3, AFT=>1, EXP=>0);
NEW_LINE;
end CENT_2_FAHR;
------------------------------------------------------------
-- FAHRENHEIT TO CENTIGRADE CONVERSION
procedure FAHR_2_CENT is
subtype FAHRENHEIT is FLOAT range -58.0..212.0;
FAHR_TEMP : FAHRENHEIT;
TEMPERATURE : FLOAT;
begin
-- Input Fahrenheit value
PUT_LINE("Input temperature in degrees Fahrenheit (float): ");
GET(FAHR_TEMP);
-- Conversion
TEMPERATURE := (FAHR_TEMP-32.0) * (5.0/9.0);
-- Output Fahrenheit value
PUT("The equivalent in degrees Centigrade is: ");
PUT(TEMPERATURE, FORE=>3, AFT=>1, EXP=>0);
NEW_LINE;
end FAHR_2_CENT;
------------------------------------------------------------
-- TOP LEVEL
begin
-- Output Menu
PUT_LINE("MENU OPTIONS");
PUT_LINE("C - Centigrade to Fahrenheit conversion");
PUT_LINE("F - Fahrenheit to Centigrade conversion");
GET(MENU_ITEM);
-- Check menu input
if (MENU_ITEM = 'C' OR MENU_ITEM = 'c') then
CENT_2_FAHR;
else
if (MENU_ITEM = 'F' OR MENU_ITEM = 'f') then
FAHR_2_CENT;
else
PUT("Invalid menu selection: ");
PUT(MENU_ITEM);
NEW_LINE;
end if;
end if;
end TEMP_CONVERT;
BVA testing: Do a BVA analysis for ranged values in two conversion procedures. A suitable set of BVA test cases is presented in the table to the right.
| TEST CASE | EXPECTED RESULT | |
|---|---|---|
| MENU_ITEM | CENT_TEMP or FAHR_TEMP | TEMPERATURE |
| c | -50.1 | CONSTRAINT_ERROR |
| C | -49.9 | -57.8 |
| c | 99.9 | 211.8 |
| C | 100.1 | CONSTRAINT_ERROR |
| f | -58.1 | CONSTRAINT_ERROR |
| F | -57.9 | -49.9 |
| f | 211.9 | 99.9 |
| F | 212.1 | CONSTRAINT_ERROR |
Limit testing: We should also derive a suitable set of test cases to exercise the limits of the input ^ values. A suitable set of test cases for this purpose is given in the table presented to the right.
| TEST CASE | EXPECTED RESULT | |
|---|---|---|
| MENU_ITEM | CENT_TEMP or FAHR_TEMP | TEMPERATURE |
| c | -50.0 | -58.0 |
| C | 100.0 | 212.0 |
| f | -58.0 | -50.0 |
| f | 212.0 | 100.0 |
Arithmetic testing: Arithmetic testing requires negative, zero and positive sample values. We have already defined test cases with negative and positive values at the limits, however a "mid range" positive and negative sample value would also be appropriate (as well as zero sample values). A suitable set of test cases is given in the table to the right.
| TEST CASE | EXPECTED RESULT | |
|---|---|---|
| MENU_ITEM | CENT_TEMP or FAHR_TEMP | TEMPERATURE |
| c | -25.0 | -13.0 |
| C | 0.0 | 32.0 |
| c | 50.0 | 122.0 |
| F | -29.0 | -33.9 |
| f | 0.0 | -17.8 |
| F | 106.0 | 41.1 |
Path testing We should test each path through the program as indicated by the flow chart presented above. From this diagram we can identify three paths. Note that where a path is dictated by a compound condition represented by a "logical or" we should test both possible conditions associated with the "or" operator. A suitable set of test cases is presented in the table to the right. Note that the first four test cases are copies of black box cases defined earlier and thus need not be run again.
| TEST CASE | EXPECTED RESULT | |
|---|---|---|
| MENU_ITEM | CENT_TEMP or FAHR_TEMP | TEMPERATURE |
| C | -25.0 | -13.0 |
| c | 50.0 | 122.0 |
| F | -29.0 | -33.9 |
| f | 106.0 | 41.1 |
| M | * | Invalid menu selection: M |
This should also be done.
Example Problem Temperature Conversion Report.
Created and maintained by Frans Coenen. Last updated 11 October 1999