REPETITION - RECURSION

2. EXAMPLE PROBLEM DECIMAL TO BINARY CONVERSION

2.1 Requirements

Develop and implement some Ada software which, when given a natural decimal number, will convert this integer into a binary number. For example, given the number 41 we would expect the system to output:

00000000 00000000  00000000 00101001

The standard mechanism, for converting from decimal to binary is to repeatedly divide the decimal number by 2 and, at each division, output the remainder (0 or 1). An example is given to the right where the binary number 101001 is derived from the decimal number 41.

2.2 Design

A top down analysis of the problem is given below.

We will implement this using the following procedures:

1. DECIMAL_2_BINARY (top level procedure): Input decimal number, call CONVERT.

   NAME	DESCRIPTION	TYPE	RANGE
   NATURAL_NUMBER	Global input variable	NATURAL	Default

2. CONVERT (Level 2 procedure): Convert to binary and output result. Call to PAD_WITH_ZEROES when necessary.

   NAME	DESCRIPTION	TYPE	RANGE
   DECL_NUM	Formal parameter	NATURAL	Default
   DIGIT_COUNTER	Formal parameter	NATURAL	Default

3. PAD_WITH_ZEROES (Level 3 procedure): Pad output with appropriate number of zeroes.

   NAME	DESCRIPTION	TYPE	RANGE
   DIG_COUNT	Formal parameter	NATURAL	Default
   END_VALUE	Local variable	INTEGER	Default

An appropriate Nassi Shneiderman design is given below.

Here we have used a recursive algorithm to ensure that the binary digits are output in the correct order. If we used a simple while loop the reverse result would be produced. A flow chart indicating the overall flow of control through the proposed software is given below.

2.3. Implementation

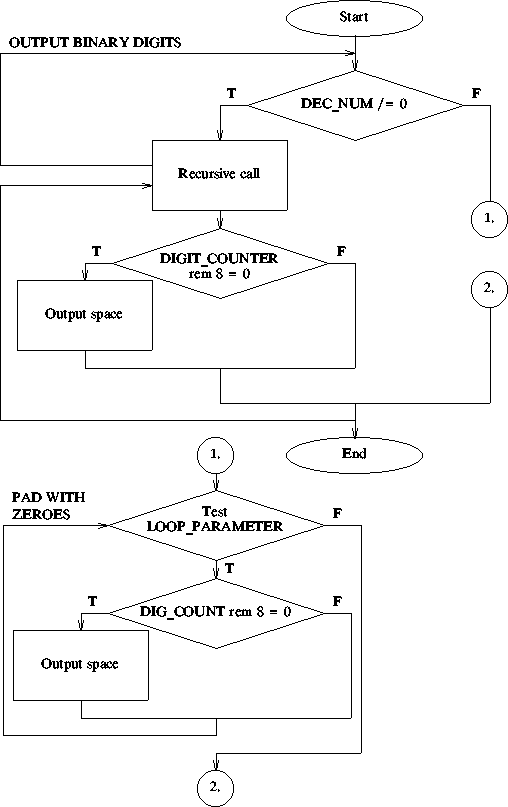
The encoding of the above design is as follows:

-- DECIMAL 2 BINARY
-- 17 September 1997
-- Frans Coenen
-- Dept Computer Science, University of Liverpool

with TEXT_IO;
use TEXT_IO;

procedure DECIMAL_2_BINARY is
    package INTEGER_INOUT is new INTEGER_IO(INTEGER);
    use INTEGER_INOUT;
    DECIMAL_NUMBER: NATURAL;

    ---------------------------------------------------------------------------
    -- CONVERT
    procedure CONVERT(DEC_NUM, DIGIT_COUNTER: INTEGER) is
        -----------------------------------------------------------------------
        -- PAD WITH ZEROES
        procedure PAD_WITH_ZEROES(DIG_COUNT: NATURAL) is
            END_VALUE: INTEGER;
        begin
            END_VALUE := 32-DIG_COUNT;
            for LOOP_PARAMETER in 1..END_VALUE loop
                PUT("0");
                if (LOOP_PARAMETER rem 8 = 0) then
                    PUT(" ");
                end if;
            end loop;
        end PAD_WITH_ZEROES;
        -----------------------------------------------------------------------
    begin
    -- Output digits and spaces between bytes when appropriate
        if DEC_NUM /= 0 then;
            CONVERT(DEC_NUM/2, DIGIT_COUNTER+1);
            PUT(DEC_NUM rem 2, WIDTH=>1);
            if (LOOP_PARAMETER rem 8 = 0) then
                PUT(" ");
            end if;
        else
            PAD_WITH_ZEROES(DIGIT_COUNTER);
        end if;
    end CONVERT;
    ---------------------------------------------------------------------------

-- TOP LEVEL
begin
    PUT("Input a natural integer: ");
    GET(DECIMAL_NUMBER);
    NEW_LINE;
    PUT(DECIMAL NUMBER)
    PUT(" = ");
    CONVERT(DECIMAL_NUMBER,0);
    NEW_LINE;
end DECIMAL_2_BINARY;

2.4. Testing

2.4.1. Black box testing

BVA, Limit and Arithmetic testing: Use BVA testing to analyse nature of inputs. Limit testing to test operation of the software at the limits, and arithmetic te sting to test the arithmetic expressions. A suggested set of test cases is given in the following Table.

2.4.2. White box testing

Path testing: We should test all paths identified in the flow charts given in Tables 3 and 4. This is already achieved by the above test cases.

Loop testing: The loop is a variable count loop therefore we should test the the loop with 1, 2 and some other number of passes through the loop. Again this will be achieved by the test cases given above.

2.4.2. Data validation testing

This should also be done.

3. EXAMPLE PROBLEM FIBONACCI

3.1 Requirements