|
|
|
Notes: (1) The example demonstrates the standard way of manipulating an array by "looping" through the array in such a manner that the loop parameter "doubles" up as the array index (or vice-versa). (2) The "setIO" code presented here is referred back to in the following lecture.
2. PREDEFINED OPERATIONS ON ARRAYS |
Some programming languages supports a number of predefined operations that can be applied to arrays. For example equality checking or concatenation. Java does not provide such operators. Java also does not support the concept of sub-arrays (sometimes referred to a slices) where a sub-array can be handled as an independent (compound) data item.
3. ARRAY VARIABLES |
|
Some imperative languages also supply a set of predefined variables (sometimes called attributes) describing various features of arrays (and indeed other data types). Typically such variables describe features such as the lower bound, upper bound and length of an array. In Java the only array variable available is length. To use this we must use the dot operator to link it to appropriate array. Thus:
int numberOfElements =
myArray.length;
|
will assign the number of elements in the array myArray to the integer data item numberOfElements. The length can be usefully used when processing arrays as shown in the example given in Table 3 where the array is processed without explicitly needing to know it length (size). The output from this code will be as follows:
doubleArray =
{0.1, 2.3, 4.5, 6.7, 8.9}
|
// USE OF ARRAY LENGTH EXAMPLE
// Frans Coenen
// Tuesday 13 April 1999
// The University of Liverpool, UK
class ArrayLengthEx {
// ------------------ METHODS -----------------------
/* Main method */
public static void main(String[] args) {
double[] doubleArray = {0.1,2.3,4.5,6.7,8.9};
int index=1;
// Output
System.out.print("doubleArray = {" + doubleArray[0]);
while(index < doubleArray.length) {
System.out.print(", " + doubleArray[index]);
index++;
}
// End
System.out.println("}\n");
}
}
|
Table 3: Use of length variable
4. MORE ARRAY PROCESSING |
We can identify a number of common operations that we may wish to perform on arrays: (1) Mapping, (2) Filtering, (3) Folding and (4) Zipping. The terminology used here is that used in declarative languages (logic and functional) to describe list handling operations. However, as arrays can be thought of as lists of elements, it seems appropriate to adopt this classification of list operations to describe common array operations. We will consider each of these operations in the following sub-sections and give an example method to be included in the Set I/O class described above.
|
It is often necessary to carry out a particular operation on all the members of an array. This is called mapping, we "map" the desired operation onto the elements of the array. For example we may wish to cube all the elements of a set (our integer array defined above) as shown in the Nassi-Shneiderman chart given in Figure 4 and the method in Table 4. |
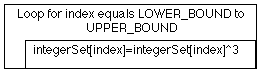
Figure 4: Nassi-shneiderman chart for cube mapping method |
/* ------ MAP CUBE ------ */
/* Cube each element of the array */
public void mapCube() {
int index;
// Loop through set array and cube each element
for(index=LOWER_BOUND;index < integerSet.length;index++)
integerSet[index] = integerSet[index] * integerSet[index] *
integerSet[index];
}
|
Table 4: Cube mapping method
|
The process of running through an array and "keeping" only those elements which pass some test is referred to as filtering. For example identifying the odd numbers in a set (integer array). A suitable SetIO method to carry this out is presented in Table 5 (associated Nassi-Shneiderman chart in Figure 5). |

Figure 5: Nassi-shneiderman chart for odd number filter method |
/* ------ ODD NUMBER FILTER ------ */
/* Loop through set array and output only those elements that represent
an odd number */
public void oddNumberFilter() {
int index, commaFlag=0;
// Loop through set array and cube each element
System.out.print("Odd numbers = {");
for(index=LOWER_BOUND;index < integerSet.length;index++) {
if (integerSet[index]%2 == 1) {
if (commaFlag == 1) System.out.print("," +
integerSet[index]);
else {
System.out.print(integerSet[index]);
commaFlag=1;
}
}
}
// End
System.out.println("}");
}
|
Table 5: Odd number filter method
|
The process of putting an operator between each pair of elements in an array to produce a single data item is called folding. For example adding up all the elements of a numeric array (set) for the purpose of finding (say) an average value or a total value. An example average method and associated Nassi-Shneiderman chart are presented in Table 6 and Figure 6, |
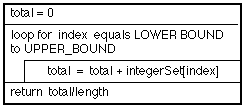
Figure 6: Nassi-shneiderman chart for average method |
/* ------ AVERAGE ------ */
/* Loop through set array and determine the total represented
by the sum of all the elements. */
public double average() {
int index, total=0;
// Loop through set array and add value of each element to total
for(index=LOWER_BOUND;index < integerSet.length;index++)
total = total + integerSet[index];
// Return
return((double) total/(double) integerSet.length);
}
|
Table 6: Average method
|
The process of combining two arrays to form a third is called zipping. For example we may wish to add the elements of two arrays to each other to form a third array (Table 7 and Figure 7). |
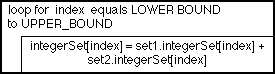
Figure 7: Nassi-shneiderman chart for zip method |
/* ------ ZIP ------ */
/* Loop through two given set arrays to form a new array. */
public void zip(SetIO set1, SetIO set2) {
int index;
// Loop through set arrays and combine each pair of elements
// to form a new element
for(index=LOWER_BOUND;index < set1.length;index++)
integerSet[index] = set1.integerSet[index] +
set2.integerSet[index];
}
|
Table 7: Zip method
Created and maintained by Frans Coenen. Last updated 10 February 2015