1. VARIABLES AND CONSTANTS

Given that we can always replace a particular bit pattern with another, the value of a data item can always be changed. Data items that are intended to be used in this way are referred to as variables. We sometimes refer to instance/class variables.

The value associated with a variable can be changed using what is called an assignment operation. In the case of Java this is indicated by the symbol `=` as illustrated previously. In Jave, by default (as is the case with many programming languages), data items are assumed to be variables. All the integer data items declared in the DataInitialisation class definition presented eralier are interpreted in this way. (The DataInitialisation instance, although also a data item, is interpreted in a different way because it is a reference to a compound data item, but more on this later.)

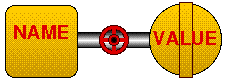
Figure 1: Constant data item (click on components!).

However it should be appreciated that what we are doing here is telling the compiler to "flag" the data item as a constant (i.e. we are only instigating software protection). Theoretically we can still change the bit pattern representing the value if we can ascertain its address, i.e. find where it is stored.

The use of named or symbolic constants offers three advantages:

It is sometimes desirable to define a data item whose value cannot be changed. Such data items are referred to as constants. In Java constants are defined by incorporating the key word final into the declaration (to indicate that they already have their "final" value!):

final int CONSTANT_DATA_ITEM = 2;

Here we have declared a constant CONSTANT_DATA_ITEM which has a value of 2. Note that by convention constant identifiers are always encoded using upper-case letters --- this allows for their easy identification, makes the code more readable and consequently more maintainable. Conceptually we can think of a constant as a data item comprising only a name and a value (i.e. no address) as shown in Figure 1.

1. By defining a symbolic constant in a single place; if that constant needs to be changed or corrected, this need only be applied to the definition and not through out the program.
2. The significance of a symbolic constant is easily understood, where as the use of a "magic number" is not so obvious.
3. The risk of miss-typing values is reduced. For example defining a constant:

   final double PI = 3.14159;
   

   reduces the risk of miss-typing 3.14159 every time it is used.

Named constants therefore enhance the maintainability of a program. Note also that fields defined within a class may also be variables or constants. We sometimes refer to instance variables/constants or class variables/constants.

2. ANONYMOUS DATA ITEMS

Often we use data items in a program without giving them a name, such data items are referred to as anonymous data items. For example in the assignment expression:

dataItem1 = 2 + (5*6);

The (5*6) part of the expression is calculated first and the result (30) stored as a data item with an address etc., but without a label (Figure 2).

Figure 2: Anonymous data item

The significance is that anonymous data items cannot be changed or used again in other parts of a program. We can think of an anonymous data item as a data item without a name, as such we cannot access its address (and hence the value stored at this address).

3. UNINITIALISED VARIABLES

In some language it is possible to define uninitialised data items, i.e. an uninitialised variable. Of course the binary digits at the indicated address will have some setting (left over from previous executions of programs) and therefore the data item will have some arbitrary value associated with it. The presence of such data items can result in errors. We can conceive of an uninitialised data item as shown in Figure 3.

Figure 3: Uninitialised data item

In Java uninitialised data items are automatically assigned a value. In the case of numeric data items the default initialisation is 0.

4. OBJECT REFERENCES

An instance of a class is a data item the same as any other (all be it an extremely complex one). When we create an instance a section of memory is set aside (on the heap) for this item. When we create an instance of a class this is the same as creating any other data item except that the immediate value associated with the data item name is an address rather than a value. This address indicates the start of the section of memory reserved in the heap for the object (Figure 4). This is because an object is what we call a compound data item in that it can have more than one value associated with it at the same time, and therefore needs a sequence of memory slots (one for each value). The immediate value associated with an instance name is thus the address of the start of this block of memory. We refer to such address values as object references (because they "reference" the start address in the heap for the values associated with the indicated compound data item). In some languages (e.g. C and C++) such data items are called pointers in that they "point" to the start of a section of memory in the heap. For example if we create an instance, newInst1, of the class ExampleClass:

ExampleClass newInst1 = new ExampleClass();

This will create a data item of the form shown in Figure 5. The data item like any other data item has an address, 100000 in the example (which is also stored on the heap), and a value (102000) which is a reference value that points to another section of the heap where the instance fields for newInst1 are stored.

Figure 5: The data item newInst1

In an earlier example we used a constructor to create an instance of the class GrandParent as follows:

Grandparent mary = new GrandParent();

Here we have created the object mary which is an instance of the class GrandParent and which has been initialised with a reference value indicating the storage location of all the associated data items.

It is possible to create an object such as mary and leave the initialisation till later. We do this using a "data declaration" of the form:

Grandparent mary = null;

the null indicates a special value, contained in the java.util package, of "nothing" (not zero but nothing!), i.e. the reference value does not point to anything.

We can have two or more names which identify the same object. For example, given the object newInst1 created above we can "assign" its immediate value (which remember is an object reference, i.e. an address) to another label as follows:

newInst2 = newInst1;

with a result as depicted in Figure 6. This is called aliasing and should be avoided as it causes confusion --- we have not made a copy of the object but created a second means of accessing it! (see Figure 6).

5. DATA TYPES

We have seen that the type of a data item defines:

1. The nature of its internal representation (number of bits).
2. The interpretation placed on this internal representation.
3. As a result of (2) the allowed set of values for the item.
4. Also as a result of (2) the operations that can be performed on it.

We have seen that the process of associating a type with a data item is referred to as a data declaration. This binds a data item name to a type definition. The process of assigning a value to a data item on declaration of that item is referred to as initialisation. (This was illustrated in the data initialisation example program presented earlier.)

Java supports eight primitive (basic) data types as summarised in Table 1. The significance of the Unicode 2.0 value associated with the char data type will be expanded upon later. The purpose of the boolean type will also be expanded upon later in the text.

All the above have specific storage and interpretation considerations associated with them and both have particular operations which may be applied to them. For example the numeric types have the + and - arithmetic operations associated with them. Note that these operations are overloaded, there is one plus operation for integer addition and one for real number addition. To mix (say) integer and real number addition - so called mixed mode arithmetic - requires special consideration (again more of this later).

6. CATEGORISATION OF TYPES

1.Pre-defined and programmer-defined types. Pre-defined types are types immediately available to the user (they are integral to the language). Programmer-defined types are types derived by the programmer using existing types (pre-defined or otherwise). Java, as is the case with many )) languages, does not provide any mechanism for fefining programmer-defined types other than classes (A class definition is a special kind of type definition). Programmer-defined types can thus be viewed as a feature of the imperative group of programming languages).

2. Scalar and Compound types. Scalar types define data items that can be expressed as single values (e.g. numbers and characters). Compound types (also referred to as composite or complex types, or object types in some OOP languages) define data items that comprise several individual values, e.g. the Java type String introduced earlier. Scalar types are generally pre-defined, while compound types are generally programmer-defined (note that the Java compound type String is predefined).

4. Primitive and Higher Level types. Primitive types (also referred to as a basic or simple types) are the standard scalar predefined types that one would expect to find ready for immediate use in any imperative programming language. Higher level types are then made up from such primitive types or other existing higher level types. Higher level types are not necessarily programmer defined - for example many languages (including Java) have a string pre-defined high-level type.

7. EXAMPLE PROBLEM --- GIANT JAVA

7.1. Requirements

To write the word "Java" vertically down the screen using giant letters made up of strings of * (asterisk) characters and blank spaces as shown in Figure 7.

Figure 7: Giant letters

7.2. System Analysis

Although there are many sophisticated object oriented techniques for analysis (and design) the simplest approach is to produce a "class diagram" of the require software system (this forms a part of many OO analysis and design techniques). A number of class diagrams have already been used in the text to illustrate various feature of Java. The simplest way of building a class diagram is to commence with a technique known as noun extraction to produce a first iteration of a class diagram --- this is a popular OO analysis technique that forms a part of many OO methodologies. The advantage is that it is a straight forward exercise, although it does require some experience of OOD and OOP to do it well. This first pass diagram can then be extended to produce a complete diagram to address the problem under consideration. The process operates as follows: Given a plain language description of a problem (i.e. a requirements statement of the above form) we extract and list the nouns in the description. Inspection of the above gives us the following: word Java screen giant letters * character blank space We then inspect this list and decide which nouns are part of the solution to the problem and which are not (some authors talk about a problem boundary, others distinguish between a solution space and a problem space). In the above case "screen" is part of the problem space and not the solution space. Be aware of synonyms -- in the above case the "word Java", "giant letters", and "* character" and "blank space" amount to the same thing (giant character of some soret). Remove nouns which are not required for the solution from the list. This then leaves us with "giant letters"

Determine which nouns describe classes of objects and which attributes. As a rule abstract nouns are usually attributes. Use this information to produce a first pass at a class diagram. In the above case we only have one noun left so this must clearly describe a class (Figure 8) Figure 8: First pass at giant letters class diagram Inspect the diagram sofar and decide if any further classes are required to produce a solution and add these to the diagram. In this case we need a second class to describe the application, we will call it the GiantJavaApp class. This ensures that there is a distinction between the giant letters class and the application which in turn will mean that we can use the GiantJava class for more than one application if we so desire. (Note: In these pages we will tend to use class names ending in "App" to indicate an application class.) Inspect the diagram again and decide if any additional attributes are needed. One approach is to return to the requirements statement and look for adjectives associated with nouns. Add class methods to the classes to produce the final version of the class diagram (Figure 9). Typically attributes will be private members which must be accessed by public methods. Therefore to assign values to the attributes associated with a class we must add appropriate class methods. In this example, reinspection of the requirements, indicates that we need methods to produce the giant letters 'J', 'A' and 'V'. Figure 9: Giant letters class diagram (final)

7.3. Design

7.3.1. GiantJava Class

Method Summary
public void	giantLetterA()            Method to output giant letter `A' to screen.
public void	giantLetterJ()            Method to output giant letter `J' to screen.
public void	giantLetterV()            Method to output giant letter `V' to screen.

The design detail required for each of the GiantJava class methods is given by the Nassi-Shneiderman charts presented in Figure 10.

Figure 10: Nassi-Shneiderman chart for GiantJava class methods

7.3.2. GiantJavaApp Class

Method Summary
public static void	main(String[] args)            Main method to create an instance of the class GiantJava and then invoke the methods giantLetterJ, giantLetterA, giantLetterV and giantLetterA to spell the word 'JAVA' down the screen.

A Nassi-Shneiderman chart for the main method is given in Figure 11. Note how method invocation (referred to as routine invocation in imperative languages) is indicated in the chart using the routine name surrounded by an ellipse. Note also that the "Draw giant letter A" operation is repeated twice.

Figure 11: Nassi-Shneiderman chart for GiantJavaApp class methods 7.4. Implementation To implement the above we must write two source files, one for the GiantJava class and one for the GiantJavaApp class. The GiantJava class source file is presented in Table 2 (compare this to the design presented in Figure 11). The application code is as presented in Table 3.

// GIANT LETTERS CLASS // Frans Coenen // University of Liverpool // 26 February 1999 class GiantJava { // -------------- METHODS -------------- /* Method to write a giant letter 'A' to the screen */ public void giantLetterA() { System.out.println(" *"); System.out.println(" * *"); System.out.println(" * *"); System.out.println(" * *"); System.out.println(" *******"); System.out.println(" * *\n\n"); } /* Method to write a giant letter 'J' to the screen */ public void giantLetterJ() { System.out.println(" *****"); System.out.println(" *"); System.out.println(" *"); System.out.println(" *"); System.out.println(" * *"); System.out.println(" ***\n\n"); } /* Method to write a giant letter 'V' to the screen */ public void giantLetterV() { System.out.println("* *"); System.out.println("* *"); System.out.println(" * *"); System.out.println(" * *"); System.out.println(" * *"); System.out.println(" *\n\n"); } } Table 2: Giant letters class

// GIANT LETTERS APPLICATION // Frans Coenen // University of Liverpool // 26 February 1999 class GiantJavaApp { // -------------------- METHODS --------------------- /* Main method to write 'JAVA' in giant letters down the screen. */ public static void main(String[] args) { // Create an instance of the class Giantletter GiantJava letter = new GiantJava(); // Invoke a sequence of methods. letter.giantLetterJ(); letter.giantLetterA(); letter.giantLetterV(); letter.giantLetterA(); } }

Table 3: Giant letters application class

javac GiantJava.java
javac GiantJavaApp.java 

   *****
     *
     *
     *
 *   *
  ***


    *
   * *
  *   *
 *     *
 *******
 *     *


*        *
*        *
 *      *
  *    *
   *  *
    *


    *
   * *
  *   *
 *     *
 *******
 *     *        

8. PROGRAM DOCUMENTATION

There is more to producing a computer solution to a problem then simply producing a well engineered piece of software that meets the requirements specification. Both the software development process and the software itself should be supported by appropriate documentation. This offers several advantages:

1. It provides for the interchange of ideas between a development team during the analysis and design phases.
2. It provides evidence that sound software engineering principles have been followed, which in turn provides support for "quality assurance".
3. It provides important information to support software maintenance.

To adhere to the above all solutions to COMP101 practical problems should be presented in the form of a "document" comprising:

1. REQUIREMENTS: A requirements statement.
2. ANALYSIS: A class diagram describing the classes required to produce a solution.
3. DESIGN: A detailed design for the class methods identified in the class diagram each comprising a data table (list of data items used in the method) and a Nassi-Shneiderman chart.
4. IMPLEMENTATION: Source code listings for each class.
5. TESTING: Tables of test cases and the output from running these test cases.