1. OVERVIEW OF ARITHMETIC OPERATORS

Arithmetic operations are among the most fundamental instructions that can be included in a computer program. Java supports all the standard mathematics operations (see Table 1).

Note that:

	Multiplication is indicated by an asterisk *.
	Division is indicated by a forward slash /.
	The % operator will compute the remainder after the division of two integer values. For example 11%2 will give 1 while 2%11 will give 2.

	When dividing one integer number (short, int or long) by another the result is always an integer. For example 5/2 will be 2 and not 2.5!
	The ++ and --, incrementation and decrementation operators, are equivalent to add or subtract one to a numeric data item. For example number++ and number-- (or ++number and --number) are equivalent to: number = number+1; number = number-1; respectively.
	The += and -= are used to add/subtract an arithmetic expression to the value of a data item. For example: number = number+(6/2); number = number-(6/2); will be equivalent to: number += 6/2; number -= 6/2;
	The ++, --, += and -= are provided as "short cuts" for frequently required arithmetic operations.

More complex arithmetic operations can be found in the Java Math class. A fragment of the Math class is given in Figure 1. The class is contained in the java.lang package which is always included in all Java programs. The class includes constants such as PI and methods such as:

	abs(float) returns the absolute value of its argument (for example Math.abs(-12.3) will return 12.3. There are abs methods for each of the primitive numeric types double, float, int and long.
	pow(double,double) which returns the value of its first argument raised to the power of the second argument. Note that both arguments are doubles.

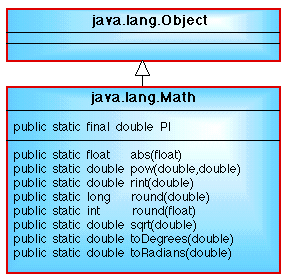
Figure 1: Math class diagram showing the fields and methods referenced here

	sqrt(double) which returns the square root of its argument (a double).
	round(double) and round(float) which return the closest long integer to the argument and the closest standard integer to the argument respectively.
	rint(double) returns the closest "integer" to its argument, but as a data item of type double.

These methods are all class (static) methods and thus we do not need to create an instance of the class Maths to use them --- we simply link them to the class name. For example:

Math.abs(number);

where number is a data item of type integer.

0.2e004

0.2e-06

2. EXAMPLE PROBLEM --- CIRCLE CALCULATION

2.1. Requirements To produce a program that calculates and outputs the circumference and area of a circle given its radius. Assume that the radius is input by the user as a double. Area of a circle = PI x diameter = 2 x PI x radius, and Circumference = PI x radius2 (Figure 2). (Use the constant PI from the Math class.)

Figure 2: Circle geometry

2.2. Analysis Using "noun extraction" the class diagram presented in Figure 3 is proposed. 2.3. Design From Figure 3 the design comprises two classes: Circle and CircleApp. 2.3.1. Circle Class

Figure 3: Circle class diagram

Nassi-Shneiderman charts for all of the above methods are presented in Figure 4.

Figure 4: Nassi-Shneiderman charts for Circle class methods

2.3.2. CircleApp Class

A Nassi-Shneiderman for the above is presented in Figure 5.

Figure 5: Nassi-Shneiderman charts for CircleApp class method

// CIRCLE CLASS
// Frans Coenen
// Tuesday 2 March 1999
// The University of Liverpool, UK

class Circle {

    // ------------------- FIELDS ------------------------               
        
    private double circleRadius;
    private double circleCircum;
    private double circleArea;
    
    // ------------------ CONSTRUCTORS -------------------
    
    /* Constructor */
    
    public Circle(double newRadius) {
    	circleRadius = newRadius;
	}
	
    // ------------------ METHODS ------------------------
    
    /* Calculate circumference */
    
    public void calcCircleCircum() {
    	circleCircum = 2.0*Math.PI*circleRadius;
    	}
	
    /* Calculate area */
    
    public void calcCircleArea() {
    	circleArea = Math.PI*circleRadius*circleRadius;
	}
	
    /* Output circumference and area */

    public String toString() {
    	return("Circumference = " + circleCircum +
	     "\nArea          = " + circleArea + "\n");
    	}
    }

// CIRCLE APPLICATION CLASS
// Frans Coenen
// Tuesday 2 March 1999
// Revised: Friday 29 March 2005, Thursday 12 May 2005
// The University of Liverpool, UK   

import java.util.*;

class CircleApp {

    // ------------------- FIELDS ------------------------    
    
    // Create instance of Scanner class

    private `static Scanner input = new Scanner(System.in);
    
    // ------------------ METHODS ------------------------  
    
    public static void main(String[] args) {
    	
	// Input radius
	
    	System.out.print("Input a radius (double): ");
	double radius = input.nextDouble(); 
	
	// Create new Circle instance
	
	Circle newCircle = new Circle(radius);
	
	// Calculate circumference and area
	
	newCircle.calcCircleCircum();
	newCircle.calcCircleArea();
	
	// Output result
	
	System.out.println(newCircle);
	}
    }

3. TRIGONOMETRIC RATIOS

Methods that return the trigonometric ratios (sine, cosine, tangent, cosecant, secant and cotangent) given an appropriate angle are all also available in the Math class. However, it should be noted that the required angle for these methods must be presented in radians and not degrees. Given an angle D (degrees) we can convert this to an angle R (radians) as follows:

R = D * Math.PI/180.0

i.e. multiply by Math.PI/180.0. To convert from radians to degree we multiply by 180.0/Math.PI. Thus:

D = R * 180.0/Math.PI

As might be expected, this is such a common operation that the Math class contains methods to do this:

1. static double toDegrees(double angrad), converts an angle measured in radians to the equivalent angle measured in degrees.
2. static double toRadians(double angdeg), converts an angle measured in degrees to the equivalent angle measured in radians.

Note that in both cases the argument and the return value are doubles. Note also that these are class methods.

An additional example problem that makes use of the trigonometric ratio methods described here is available.