|
|
|
The first three examples programmes illustrate fixed count pre-test loops using the "for" construct. The first example problem (ASCII character set) also includes a fixed count pre-test "for" loop. The second example problem (arithmetic progression) makes use of a variable count pre-test loop using a "for" construct.
1. REPETITION |
|
A repetition construct causes a group of one or more program statements to be invoked repeatedly until some end condition is met. The condition comprises a Boolean expression of some form. In this respect repetition constructs have three elements:
|
We can identify two main forms of repetition:
To which we could add recursion (routine calls itself). We will confine the following discussion to fixed and variable count loops and briefly describe recursion at a later date. |
1.1. pre-test and post-test loopsIn addition both loops can be further classified according to whether they are pre-test or post-test loops. In the case of a pre-test loop the end condition is tested for prior to each repetition, while in the case of a post-test loop the end condition is tested for after each repetition. With respect to Java pre-test fixed and variable count loops are supported as well as post test fixed and variable count loops. Languages such as C and C++ support a similar set of loops, while languages such as Ada only support pre test loops. |
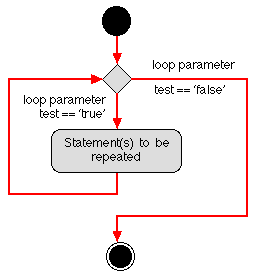
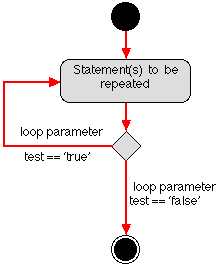
We can illustrate the distinction between pre-test and post-test loops by considering the flow of control associated with each. In the case of a pre-test loop we test before entering the "repeat" statement, thus if on the first attempt the test fails no repetitions will be made; in the case of a post-test loop the "repeat" statement is called at least once. We can conceive of flow of control in terms of a floor plan comprising "rooms", "lobbies" and "corridors"; where "rooms" represent program statements, "lobbies" represent choice points, and "corridors" the connections between statements. We can then (in virtual terms) "run" round the floor plan simulating the flow of control. The floor plans given in Figure 1 thus simulate the flow of control that differentiates a pre-test loop from a post-test loop. Generic activity diagrams for the pre- and post-test loop constructs are presented in Figure 2. |
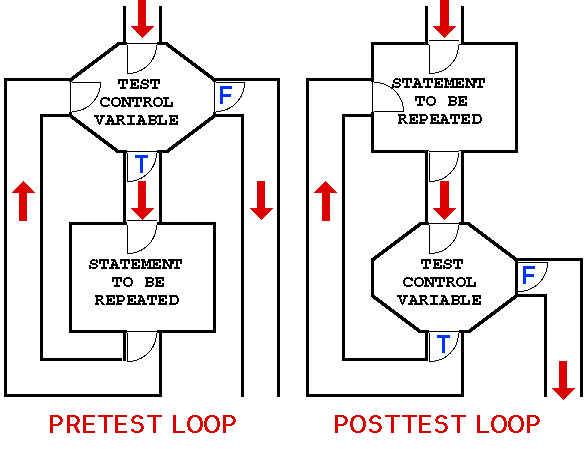
Figure 1: Distinction between pre-test and post-test loops
(a) |
(b) |
Figure 2: Generic activity diagrams for pre-test and post-test loops
2. LOOPS IN JAVA |
|
From the above we can therefore identify four basic types of loop:
In Java (in common with languages such as C and C++) things are not so clear cut. Java supports three types of loop construct: |
Thus we have two mechanisms for constructing variable and fixed count pre-test loops; which to use and when is entirely up to the whim of the programmer! |
3. FOR LOOPS IN JAVA |
|
The general form of a for loop in Java is:
for ( < startExpression > ;
< testExpression > ;
< updatExpression > ) {
< sequence of statements >
}
(Note the semi-colons.) This is a very concise (compared to languages such as Pascal and Ada), method of defining a loop (similar to that found in C and C++) that is sometimes criticised because of its lack of easy interpretation (there is always a trade off between conciseness and understandability). The counter-argument to this is that this form of loop definition is much more versatile than that available in (say) Ada. What ever the case, from the above:
|
Note: loop parameters are usually of some scalar numeric type. It is good practice to use parameters of type int or long. This is because real numbers have machine dependent precision associated with them, which may result in loops behaving in an unexpected manner as a result of inexact comparison of the loop parameter with some end condition. In Table 1 a trivial Java program is presented, incorporating a loop, which outputs a sequence of 10 "smiley faces": (-: (-: (-: (-: (-: (-: (-: (-: (-: (-: Note that the start and end values for the loop are defined as constants and not as magic numbers. This is for sound software engineering reasons because the use of a name conveys much more meaning to a reader than a number. |
// SMILEY FACE APPLICATION CLASS
// Frans Coenen
// Tuesday 13 April 1999
// The University of Liverpool, UK
class SmileyFace {
// ------------------ METHODS -----------------------
/* Main method */
public static void main(String[] args) {
int loopParameter;
final int START_CONDITION = 0;
final int END_CONDITION = 10;
// For loop
for (loopParameter = START_CONDITION;loopParameter < END_CONDITION;
loopParameter++)
System.out.print("(-:\t");
// End
System.out.println("\n");
}
}
|
Table 1: Java for loop example
In the example the loop parameter is declared before the loop construct and assigned to within the construct. We could have initialised the loop parameter entirely within the loop construct as follows:
for (int loopParameter = START_CONDITION;loopParameter < END_CONDITION; loopParameter++)
4. USING THE LOOP PARAMETER |
In the example given in Table 1 the loop parameter serves no other purpose than to control the loop. In addition we can make use of the parameter as (say) part of an output statement, or as part of some simple arithmetic. Table 2 gives an example of the first, and Table 3 an example of the second. The code in Table 2 is used to simply output a sequence of numbers (the loop parameter):
0 1 2 3 4 5 6 7 8 9
The code in Table 3 performs some arithmetic on the loop parameter so that a sequence of even numbers is produced:
0 2 4 6 8 10 12 14 16 18
// SEQUENCE NUMBERS CLASS
// Frans Coenen
// Tuesday 13 April 1999
// The University of Liverpool, UK
class SequenceNumbers {
// -------------- METHODS -------------------
/* Main method */
public static void main(String[] args) {
final int START_CONDITION = 0;
final int END_CONDITION = 10;
// For loop
for (int loopParam = START_CONDITION;loopParam < END_CONDITION;
loopParam++)
System.out.print(loopParam + " ");
// End
System.out.println("\n");
}
}
|
Table 2 Sequence of numbers
// SEQUENCE EVEN NUMBERS CLASS
// Frans Coenen
// Tuesday 13 April 1999
// The University of Liverpool, UK
class SequenceEvenNumbers {
// -------------- METHODS -------------------
/* Main method */
public static void main(String[] args) {
final int START_CONDITION = 0;
final int END_CONDITION = 10;
// For loop
for (int loopParam = START_CONDITION;loopParam < END_CONDITION;
loopParam++)
System.out.print(loopParam*2 + " ");
// End
System.out.println("\n");
}
}
|
Table 3 Sequence of even numbers
The same result as that produced by the code in Table 3 can be achieved by rewriting the method as follows:
public static void main(String[] args) {
final int START_CONDITION = 0;
final int END_CONDITION = 19;
// For loop
for (int loopParam = START_CONDITION;loopParam < END_CONDITION;
loopParam = loopParam+2)
System.out.print(loopParam + " ");
// End
System.out.println("\n");
}
6. EXAMPLE PROBLEM - ARITHMETIC PROGRESSION (Variable count pre-test "for" loop example)6.1 RequirementsDesign and implement a Java program that outputs the first N terms of an a.p. (arithmetic progression) of the form: where A is the first term and D is the common difference. 6.2 AnalysisA class diagram for the proposed solution is given in Figure 6. Note that a total of three classes are proposed. A general class Progression, a sub class of this class called ArithmeticProg, and an application class --- ArithmeticProgApp. 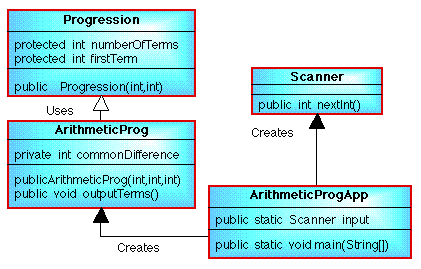
Figure 6: Arithmetic progression application class diagram 6.3 Design6.3.1 Progression Class
A set of Nassi-Shneiderman charts for the above methods is presented in Figure 8. 
Figure 8: Nassi-Shneiderman charts for ArithmeticProg class methods 6.3.3 ArithmeticProgApp Class
Table 6: Progression and arithmetic progression classes 6.4.2 ArithmeticProgApp class
Table 7: Arithmetic progression application classes 6.4. Testing6.4.1. Black box testingArithmetic Testing: We should test inputs with negative, zero and positive sample values. A suitable set of test cases is given below. Note that a zero or negative input for "number of terms" will result in no output because the loop is never exercised. Note also that with this many test cases a test harness program seems like a good idea. Some suitable code is presented in Table 8.
Table 8: Test harness code for arithmetic progression application program 6.4.2. White box testingLoop testing: Where the user controls the number of repetitions in a variable count loop the loop should be tested (in theory) as follows:
The nature of our implementation is such that we do not have a particular end value in mind and thus we cannot define tests related to this, however, the set of tests given in the table below are appropriate in this case.
Just for interest the output for 100 terms with a start value of -40 and a common difference of 3 is presented in Table 9.
Table 9: Example output from arithmetic progression application program | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Created and maintained by Frans Coenen. Last updated 10 February 2015