INTRODUCTION TO PROGRAMMING IN JAVA: REPETITION AND RANDOM NUMBER GENERATION

NOTE: This set of www pages is not the set of www pages for the curent version of COMP101. The pages are from a previous version that, at the request of students, I have kept on line.

1. Random numbers
2. Example problem - Random number generator

3. Alternative random number generator

The random number generator example problem uses all three loop constructs in a variety of variable count modes. Also uses a class constant and a class method; up to this point, although we have used class constants and methods from the Java API (particularly with respect to the Math class) we have not created such class members ourswelves.

1. RANDOM NUMBERS

To produce random numbers using a computer we generate a series of numbers:

N₀, N₁, N₂, N₃, ...

that appear to be random. A common equation used to generate such a series is:

N_i+1 = (KxN_i) % M

where % is the remainder operator, K and M are constants, N_i is the current term (random number) and N_i+1 is the following term. This equation requires a start term (N₀), often referred to as the seed, after which subsequent terms can be generated. To ensure realistic operation of the equation appropriate values for K and M are also required.

For example if N0=3, K=5 and M=4 all the terms will be equivalent to 3 ((5x3) % 4 = 3). Theories exist on the best choice of values for K and M, Skansholm (1997) suggests:

K = 5⁵ = 3125

M = 2¹³ = 8192

and a seed with an odd number value within the range of 1..M-1 (i.e. 1..8191). This will then produce a series of "random" numbers within the range 1..M-1 (i.e. 1..8191). If we wished to produce random numbers between say 0..99 or 0..9 (inclusive) we would have to apply appropriate corrections:

100/M                or              10/M

1.1 Alternative Random Number Generation Algorithms

The above is only one example of how random numbers may be generated, there are many others. For example Clocksin and Mellish (1984) suggest the following:

N_i = (S_i%R) + 1

Where S_i is the seed. This then produces random numbers between 1 and R. Note that N_i is not dependent on the value of the previous number in the series (N_i-1), instead the seed (S) is recalculated on each iteration. Clocksin and Mellish suggest the following identity to achieve this:

S_i+1 = ((125xS_i)+1) % 4096

2. EXAMPLE PROBLEM RANDOM NUMBER GENERATOR

2.1 Requirements

Develop and produce a program that generates a series of random numbers between 0 and 99 inclusive until the number 50 is generated. Use the equation:

N+1 = 3125xN % 8192

where:

	`N` is the current term.
	`N+1` is the following term.

Note that to start the series we require an initial value for N which must be an odd number between 1 and 1891. Note also that the equation will produce terms ("random numbers") within the range 1 to 8191 therefore to produce random numbers within the range 0 to 99 inclusive we must multiply the result by 100/8192.

2.2 Analysis

We will create a separate class Random Generator which will contain the code to generate a random number. The particular application in question (generate random numbers between 0 and 99 until a number 50 is produced will be contained in a second class, RandomApp, which will contain a "do-while" loop and allow the user to set the seed. A class diagram is presented in Figure 1. Input, where necessary will be facilitated through the numeric input class defined earlier.

Figure 1: Class diagram for random number generator problem

2.3 Design

2.3.1 `RandomGenerator` class

Field Summary
`private static final int`	`M_CONSTANT` A class constant for "M" set to `2¹³`.
`private static final int`	`K_CONSTANT` A class constant for "K" set to `5⁵`.
`private int`	`term` An instance variable to store the current random number.

Constructor Summary

RandomGenerator(int seed)
Constructor to create an instance of the class RandomGenerator given a particular seed.

Method Summary
`public int`	`randomNumber()` Method to return a random number between `1` and `1891`.
`public static int`	`getMconstant()` Public "get" class method to access and return the `M_CONSTANT` private class data member in the `RandomGenerator` class.

2.3.2 `RandomApp` class

Field Summary
`public static Scanner`	`keyboardInput` A class instance to facilitate input from the input stream.

Method Summary
`public static void`	`main(String[] args)` Main method for random number application.
`private static void`	`inputSeed()` Method to allow user to input an appropriate seed. Includes a "do-while" loop to facilitate error detection and recovery.

A set of Nassi-Shneiderman charts describing the above operations is given in Figure 2.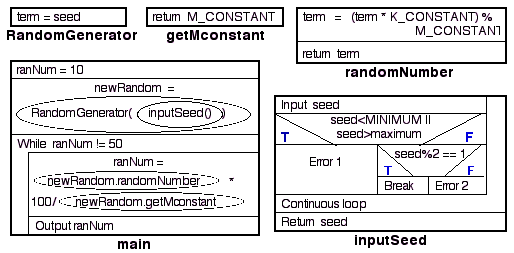

Figure 2: Nassi-Shneiderman charts for random number problem solution

2.4 Implementation

2.4.1 `RandomGenerator` class

// RANDOM GENERATOR
// Frans Coenen
// Monday 21 June 1999
// The University of Liverpool, UK   

class RandomGenerator {

    // ------------------- FIELDS ------------------------
             
    private static final int M_CONSTANT = 8192;		// 2^13
    private static final int K_CONSTANT = 3125;     	// 5^5
    private int term;         
    
    // ---------------- CONSTRUCTORS ---------------------
    
    /* Random Generator constructor */
                        
    public RandomGenerator(int seed) {
        term = seed;
        }
	
    // ------------------ METHODS -----------------------

    public int randomNumber() {	
	term = (term * K_CONSTANT) % M_CONSTANT;
        return(term);
    	}
	
    // ----------------- GET M CONSTANT ------------------
    
    public static int getMconstant() {
    	return(M_CONSTANT);
	}
    }

Table 1: Source code for random number generator class

2.4.2 `RandomApp` class

// RANDOM NUMBER APPLICATION
// Frans Coenen
// Monday 21 June 1999
// Revised: Wednesday 24 August 2005
// The University of Liverpool, UK   

import java.util.*;

class RandomApp {
    
    // ------------------- FIELDS ------------------------ 
                                           
    // Create Scanner class instance
    public  static Scanner keyboardInput = new Scanner(System.in);
			 
    // ------------------- FIELDS ------------------------ 
	
    /* Main method */
    
    public static void main(String[] args) {
        int ranNum = 10;
	final int END_CONDITION = 50;
	
	// Create an instance of the class Random.	
	RandomGenerator newRandom = new RandomGenerator(inputSeed());
	
	// Generat random numbers until a random number equivalent to 
	// 50 has been produced.	
	while (ranNum != END_CONDITION) {
	    ranNum = newRandom.randomNumber()*
	                      100/(RandomGenerator.getMconstant()-1);
	    System.out.print(ranNum + " ");
    	    }
	    
	// End
	
	System.out.println();
        }

    /* Input seed for random number generator */
    
    private static int inputSeed() {
	int seed;
	final int MINIMUM = 1;
	int maximum = RandomGenerator.getMconstant();
	
	// Invitation to input
        System.out.println("Input an odd integer between " + MINIMUM + 
				" and " + maximum + " (inclusive)");

        // Do-while loop
        do {
            seed = keyboardInput.nextInt();
	    if (seed < MINIMUM || seed > maximum) 
	    		 System.out.println("ERROR 1: Input " + seed +
			                 " out of range, try again!"); 
	    else {
	        if (seed%2 == 1) break;
	        System.out.println("Error 2: Invalid input " + seed + 
			               " (even number), try again!");
		}	
            } while (true);

        // Return  
	return(seed);
	}    
    }

Table 2: Source code for random number application class

2.5 Testing

There are two loops in the above code, one exits when a random number equal to 50 is encountered and is beyond our control. The other checks for an appropriate seed. Given that we know the required range for the input seed we can carry out both BVA and limit testing on this range. For good measure we should also test a seed with a value somewhere in the middle of the prescribed range. An appropriate set of test cases are presented below with a set of test results in Table 3.

TEST CASE	EXPECTED RESULT
decimalNumber	OUTPUT
0	ERROR 1, Out of range
8192	ERROR 1, Out of range
2	ERROR 2, Even number
8190	ERROR 2, Even number
1	Random number sequence
8191	Random number sequence
4095	Random number sequence

$ java RandomApp
Input an odd integer between 1 and 8191 (inclusive)
0
ERROR 1: Input 0 out of range, try again!
8192
ERROR 1: Input 8192 out of range, try again!
2
Error 2: Invalid input 2 (even number), try again!
8190
Error 2: Invalid input 8190 (even number), try again!
1
38 9 29 69 12 73 56 66 78 41 48 42 84 62 55 46 81 86 29 27 18 63 
17 37 46 44 72 25 14 77 42 42 74 13 78 36 73 3 29 58 64 96 46 59 
95 42 79 88 17 91 77 95 79 93 91 30 32 98 70 43 25 57 65 84 10 
18 26 3 34 33 3 51 50
$ java RandomApp
Input an odd integer between 1 and 8191 (inclusive)
8191
61 90 70 30 87 26 43 33 21 58 51 57 15 37 44 53 18 13 70 72 81 
36 82 62 53 55 27 74 85 22 57 57 25 86 21 63 26 96 70 40 35 3 53 
40 4 57 20 11 82 8 22 4 20 6 8 6 9 67 1 29 56 74 42 34 15 89 81 
73 96 65 66 96 48 49 48 54 23 93 78 97 69 47 3 74 37 59 76 35 77 
81 46 30 39 63 63 10 73 54 76 24 29 4 36 23 56 63 94 56 6 82 98
73 27 11 99 25 70 98 47 61 85 95 91 32 22 52 83 87 31 18 71 76 
61 43 7 50
$ java RandomApp
Input an odd integer between 1 and 8191 (inclusive)
4095
11 40 20 80 37 76 93 83 71 8 1 7 65 87 94 3 68 63 20 22 31 86 32 
12 3 5 77 24 35 72 7 7 75 36 71 13 76 46 20 90 85 53 3 90 54 7 
70 61 32 58 72 54 70 56 58 19 17 51 79 6 24 92 84 65 39 31 23 46 
15 16 46 98 99 98 4 73 43 28 47 19 96 53 24 87 9 26 85 27 31 96 
80 89 13 13 60 23 4 26 74 79 54 86 73 6 13 44 6 56 32 48 23 77 
61 49 75 20 48 97 11 35 45 41 82 72 2 33 37 81 68 21 26 11 93 57 
0 14 27 89 8 38 21 68 0 35 25 44 27 53 87 67 38 43 59 87 83 55 
91 53 13 39 32 17 77 44 32 27 26 22 41 34 9 21 10 88 76 92 89 39 
78 86 26 37 64 51 73 32 85 38 80 74 90 96 96 12 29 77 71 97 53 
30 55 80 11 4 99 9 53 50

Table 3: Test results

Note that a seed of 59 will rerturn 50 straight away!

3. ALTERNATIVE RANDOM NUMBER GENERATOR

Although it is instructive to examine how computers can generate "random numbers", one of the central features of languages such as Java is code reuse. Therefore if a suitable predefined method exist in the Java SDK (Java Software Development Kit) then we should use this method. Inspection of the Math class indicates that there is a random() which returns a double greater than or equal to 0.0 and less than 1.0. An alternative random number application class which uses this method is presented in Table 4 below.

// RANDOM NUMBER APPLICATION 2
// (Using built-in generator supplied by the JDK)
// Frans Coenen
// Friday 15 September 2000
// The University of Liverpool, UK   

class RandomApp2 {
    
    /* Main method */
    
    public static void main(String[] args) {
        int ranNum  = 10;	// Set first random
	
	// Generate random numbers until a random number  
	// equivalent to 50 has been produced.	
	for( ;ranNum!=50; ) {
	    ranNum = (int) (Math.random()*100);
            System.out.print(ranNum + " ");
    	    }
	    
	// Return	
	System.out.println();
        }
    }

Table 4: Source code for random number application class (version2)

Note that the code presented in table 4 makes use of a "for" loop, we could equally well have used a "while" loop:

while (ranNum != 50) {
    ranNum = (int) (Math.random()*100);
    System.out.print(ranNum + " ");
    }

Some example output produced by the above code is given in Table 5.

$ java RandomApp3
36 52 48 60 13 24 89 68 31 63 23 41 6 54 97 43 95 40 94 71 85 17 10 22
3 44 5 48 14 57 2 29 82 82 68 79 73 4 52 75 27 16 82 12 5 72 5 77 90 49 
54 20 0 3 59 28 60 3 71 95 36 21 60 85 83 57 53 25 47 61 35 46 1 48 93 
30 2 79 88 36 94 19 61 97 97 64 44 20 60 82 22 41 3 5 6 12 72 38 4 74 32 
92 75 47 90 50

$ java RandomApp3
89 76 5 42 82 56 66 75 45 38 49 24 47 3 89 11 98 75 48 54 16 92 44 30 
36 44 9 16 66 1 26 85 23 99 43 55 66 62 47 48 6 48 5 37 43 25 89 20 5 
82 19 83 41 77 81 14 78 15 10 91 0 62 27 53 6 26 94 77 18 92 39 0 66 5 
79 7 52 82 67 21 70 27 91 83 72 31 22 62 89 12 34 12 95 23 24 69 99 44 
21 90 31 47 47 90 10 59 58 47 45 37 15 41 75 28 74 56 6 79 84 35 68 87 
6 2 69 60 23 76 5 92 90 57 37 33 62 97 37 4 31 6 64 32 74 82 21 39 35 
26 22 62 18 97 81 21 34 15 35 41 56 29 87 31 43 12 54 79 11 97 29 51 13 
65 19 19 47 4 65 25 83 33 43 61 71 14 51 2 50

$ java RandomApp3
25 86 69 90 38 60 18 49 30 70 21 75 16 90 44 99 25 30 6 46 77 95 61 98 
92 42 42 0 47 6 45 26 60 85 92 96 68 44 56 97 74 12 86 54 26 66 90 7 
51 10 88 37 84 81 1 93 25 46 49 96 81 21 92 41 21 40 96 83 82 25 1 23 
91 15 44 86 4 99 17 58 8 5 43 26 41 48 12 22 98 23 81 18 77 87 66 64 
65 24 22 0 47 2 22 81 31 17 39 70 82 73 9 78 93 4 63 88 75 32 4 17 84 
48 85 32 19 83 30 3 66 12 57 24 24 10 7 4 20 9 83 48 13 75 17 71 88 53 
10 41 48 45 23 9 91 18 45 29 38 34 72 32 35 19 60 18 35 25 81 84 66 94 
73 92 13 20 59 19 42 48 6 64 87 32 31 69 30 69 52 67 24 13 71 48 63 53 
18 9 46 85 48 57 83 84 22 18 25 15 46 6 81 57 48 34 26 60 20 58 6 38 4 
49 51 54 86 62 93 4 23 94 80 38 66 30 42 11 15 16 17 35 35 74 41 70 48 
97 84 29 36 14 29 38 24 20 32 0 64 16 20 52 77 67 52 21 36 25 53 67 2 
14 95 31 1 98 29 65 4 60 63 12 40 58 56 58 13 88 4 66 81 16 6 1 19 74 
30 58 24 44 61 72 2 65 50

Table 5: Sample output from random number application class (version 2).

REFERENCES

Clocksin, W.F. and Mellish, C.S. (1984). Programming in Prolog, 2nd Edition. Springer-Verlag.
Skansholm, J. (1997). Ada 95 From the Beginning, 3rd Edition. Addison-Wesley.

Created and maintained by Frans Coenen. Last updated 10 February 2015