1. INTRODUCTION TO DATA TYPES

The type of a data item defines:

1. The nature of its internal representation.
2. The interpretation placed on this internal representation.
3. As a result of (2) the allowed set of values for the item.
4. Also as a result of (2) the operations that can be performed on it.

The process of associating a type with a data item is referred to as a data declaration.

Categorisation of Types

2. Scalar and Compound types. Scalar types define data items that can be expressed as single values (e.g. numbers and characters). Compound types (also referred to as composite or complex types) define data items that comprise several individual values. scalar types are generally pre-defined, while compound types are often programmer-defined.

3. Discrete and Non-discrete types. Discrete types (also refered to as linear or ordinal tpes) are types for which each value (except its minimum and maximum) has a predecessor and a successor value. The opposite are referred to as non-discrete types.

4. Basic and Higher Level types. Basic types (also refered to as a simple types or type primitives) are the standard scalar predefined types that one would expect to find ready for imediate use in any imperative programming language. Higher level types are then made up from such basic types or other existing higher level types. Higher level types are not necessarily programmer defined - for example many imperative languages include a string high-level type.

2. STANDARD PREDEFINED (BASIC) TYPES

Every imperative languages supports a number of standard basic data types:

Note that the type void supported by C indicates a type whose value corresponds to "nothing".

Examples of Data Item Initialisation in Ada and C

Note that Ada supports multiple initialisation (e.g. NUM_C, NUM_D: integer:= 3;) while C does not.

3. RANGE AND PRECISION WITH RESPECT TO NUMERIC TYPES

• The term range refers to the minimum and maximum value that numeric types can take.
• The term precision refers to the number of significant figures with which a numeric type is stored.
• All numeric types have default precisions and/or ranges associated with them.
• Different imperative languages specify ranges and precisions in different ways, but there are three principal styles:
  1. Predefined (cannot be influenced by the programmer)
  2. Adjectives (e.g. C)
  3. Explicit specification (e.g. Ada, Pascal)

Adjectives

Adjectives are used to specify classes of numeric types. Some C examples are given below:

4. POINTERS AND ACCESS VALUES

Pointers are variables that have as their value an address, i.e. a reference to another data object (Fifure 1). The consequence of this is that we have a second "access" route to Value 2 in Figure 1; the standard route through Name 2 and a second rout by dereferencing the Valu 1 accessed through Name 2.

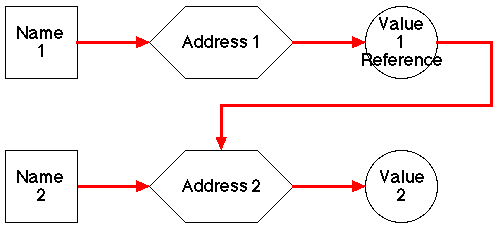
Figure 1: C POINTER>

• A pointer may take a special value null which indicates that the pointer is pointing nowhere.
• Given a pointer we can access the value "pointed" to through a process known as dereferencing.

C POINTERS

• C makes extensive use of pointers and uses two prefix operators:

  * (Asterisk)
  & (Ampersand)
  

• * when used in a declaration is read as "pointer to a data type". Example:

  int *numberPtr;
  

• * when used elsewhere is interpreted as "the value contained in the reference/ address pointed at" (i.e. the pointer is dereferenced). Example:

  *numberPtr = *numberPtr + 1;
  

• & when used anywhere is read as the "reference/address of ...". Example:

  numberPtr = &x
  

  In this case x is referred to as a reference variable.

Consider the following C example:

#include 

void main(void)
{
int n, *nptr;

n = 2;
nptr = &n;
printf("n = %d\(bsn",n);
printf("address of n = %d\(bsn",&n);
printf("nptr = %d\(bsn",nptr);
printf("address of nptr = %d\(bsn",&nptr);
printf("value pointed at = %d\(bsn\(bsn",*nptr);

n = 4;
printf("n = %d\(bsn",n);
printf("address of n = %d\(bsn",&n);  
printf("nptr = %d\(bsn",nptr);
printf("address of nptr = %d\(bsn",&nptr);
printf("value pointed at = %d\(bsn\(bsn",*nptr);
}     

This will output the following:

n = 2
address of n = 2063808352
nptr = 2063808352
address of nptr = 2063808356
value pointed at = 2

n = 4
address of n = 2063808352
nptr = 2063808352
address of nptr = 2063808356
value pointed at = 4    

Note that the address of number and the value of numberPtr are the same. We can illustrate this as shown in Figure 2.

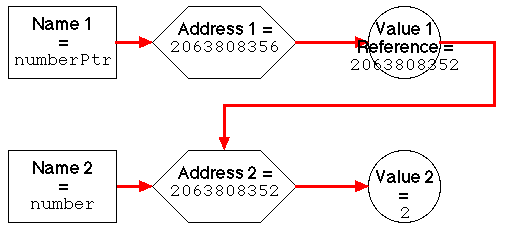
Figure 2: C POINTER EXAMPLE>

5. TYPE DECLARATIONS

There are many situations where it is desirable for programmers to define their own types:

1. To enhance clarity and readability.
2. To obtian better representation of reality.
3. To facilitate automatic checks on values.

Not all languages support the concept of programmer defined types (Ada and Pascal do, C does not --- C allows renaming of type definitions which is not wuite the same thing). Where supported orogrammer-defined types are presented using a type declaration statement. This binds a "new" type definition with a type name (remember that a data item declaration statement binds a data item name to a type definition). In Ada and Pascal type declaration statements have the general form:

type <TYPE_NAME> is <TYPE DEFINITION> ;

<TYPE_NAME> = <TYPE DEFINITION> ;

Note that in Pascal type declarations must be grouped together in a type declaration section which must be preceded by a const declaration section (if any), and followed by a var declaration section (again if any).

Ada example type declarations incorporating specific ranges and/or precisions:

type SCORE is range 0 .. 100 ;

type TEMPERATURE is digit 3 ;

type PERCENTAGE is digits 4 range 0.0 .. 100.0

Note that in each case the Ada compiler will deduce that the types SCORE and TEMPERATURE are integewr types and that the type PERCENTAGE is a floating point type. Once the above types have been declared they can be utilised in the usual manner:

A_VALUE : SCORE ;

SUMMER : TEMPERATURE := 20 ;

X_VALUE, Y_VALUE : PERCENTAGE := 100.0;

If in the above declarations, an attempt is made to assign a value outside the specified range an error will result.

6. ALIASING (RENAMING) TYPE NAMES

It is sometimes desirable, given a particular application, to use more descritive (application dependent) type names for particular types. Again this offers advantages of:

1. Clarity
2. Brevity

In Ada this is achieved using a type declaration statement (see above):

subtype REAL_T is float;
NUMBER: REAL_T;

In C a type definition construct is used. This has the general form:

typedef <DEFINITION> < NAME OR NAMES>

Example:

typedef float REAL, *REALPTR;
REAL x;
REALPTR xPtr; 

In both of the above examples an alternative name for the type "float" has been declared. In addition, in the C example, a pointer to the new type has also been declared. Note that by convention, in C, alternative names are typed in uppercase.

7. ADA ACCESS VALUES

Languages such as Ada and Pascal do not specifically support the concept of pointers as used in C, however itb is possible to define a variable that has as its value an address (reference). Such data items are known as access ir reference variables (the concept also exists in Java).To declare an access value the reserved word access is used in the declaration. Example:

with CS_IO; use CS_IO;

procedure ACCESS is
   type INTEGERPTR is access
      integer;
   INT_PTR: INTEGERPTR:=
      new integer'(2);
begin
   put(INT_PTR.ALL); new_line;
end ACCESS;

7. SUB-TYPES

Given a particular application it is sometimes also useful to characterise a sub-set of values of some other pre-existing type. This is supported by languages such as Ada (but not C) where a subtype declaration statement is used as follows:

subtype DAY_NUMBER_T is integer
        range 1..31;
DAY: DAY_NUMBER_T:= 10;

Here the type DAY_NUMBER_T is declared as a "sub-type" of the type integer (the new types range is a sub-set of that available for the supper-type). A similar effect can be achieved in Pascal (although the languages does not specifically support a "subtype" statement).

Some imperative languages that support the concept of sub-types also provide some predefined ("built-in") sub-types. For example Ada supports two predefined sub-types. For example Ada supports two predefined sub-types of the type INTEGER which are defined as follows:

subtype NATURAL is INTEGER range 0..INTEGER'LAST;

subtype POSITIVE is INTEGER range 1..INTEGER'LAST;

(note the use of the integer attribute last). Use of subtypes offers similar advantages to those associated with the use of programmer defined types:

1. Readability.
2. Good representation of reality.
3. Error checking.

7.1. When to use Type and Subtype Declarations

Both offer similar advantages when many computations. However, generally speaking, where a data item is required to display many of the features of the standard INTEGER or FLOAT types a subtype declaration should be used. Type declarations are usually used to describe what are termed compound types (e.g. arrays), but more on this later.

8. MACRO SUBSTITUTION

Macro substitution is where some string replaces every occurrence of an identifier in a program. This is supported by C (but not Ada or Pascal). To define a macro substitution we include a statement at the beginning of our C program of the form:

#define < macro name> < macro string>

For example:

#define TRUE 1

will replace the identifier true, where ever it occurs within the program, with the string 1 during compilation.