Introduction

In Lecture 4 one of the standard data structures for representing Undirected Graphs was presented.

One weakness of the technique used, is that a 2-dimensional array is not an efficient way to hold details about graphs which do not have `many' edges, (so-called sparse graphs),

In order to overcome some of the problems with the adjacency matrix representation (as the technique used in Lecture 4 is known), an alternative approach (called incidence list representation) can be used.

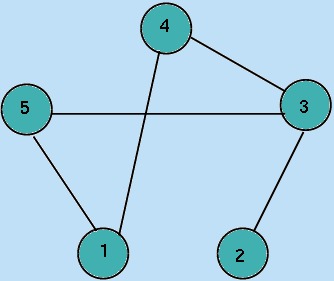
For the graph,

The adjacency matrix (2-D array) form would be:

whereas the incidence list form would be:

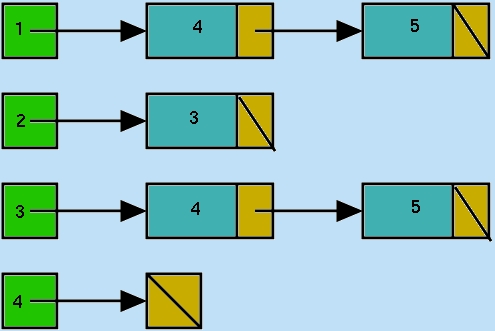So if G(V,E) is an n-vertex undirected graph with vertex set

The incidence list representation of G(V,E) uses:

An array of n-1 Linked Lists.

(One linked list for each of the vertices v such that 1< = v < n.)

The linked list for vertex k has one list cell for each vertex, w for which:

(if there are no such edges the corresponding linked list is empty).

Requirements

Design, implement and test a Java Class, SparseGraph, whose Class Diagram is

Description

Class Fields

• private EdgeList [ ] Incidence

  Incidence is an array of EdgeList that will hold the Graph. The class EdgeList is the Linked List Class described in Lecture 6, but changed so that a List cell has two fields (as before):

  int Node

  ListCell Link

  i.e. The data held in an EdgeList is always of type int rather than an arbitrary Object class.

  You do not have to implement the class EdgeList.

  An implementation of this can found obtained here.

• private int Order

  Records the number of vertices in this SparseGraph instance. Hence Incidence[] when instantiated will be an array of Order-1 EdgeLists.

• private int Size

  Records the number of edges in this SparseGraph instance.

Constructors

• public SparseGraph (int n)

  The parameter n defines the number of vertices in this instance. The fields should be instantiated so that Order is set to n; Size to 0; and Incidence as an array of n-1 new instances of EdgeList.

• public SparseGraph (int [][] Mat, int n)

  n is the number of vertices in this instance (so Order=n)

  Mat is assumed to be 2-dimensional array with n rows and n columns; the field Incidence is instantiated to represent the undirected n-vertex graph that Mat describes as follows:

  1. For all 1<= i <= n Mat[i][i] = 0
  2. For all 1 <= i < j <= n: Mat[i][j] = Mat[j][i];
  3. If Mat[i][j] > 0 the graph contains an edge between vertex i and vertex j. If Mat[i][j] <= 0 there is no edge connecting vertices i and j.

  (N.B. Mat[][] is just an adjacency matrix representation of some Graph)

  The SparseGraph instance formed by this constructor should correspond to the incidence list representation of the graph whose adjacency matrix is Mat.

Instance Methods

• public int OrderOf()

  Returns the value of the field Order for this instance.

• public int Sizeof()

  Returns the value of the field Size for this instance.

• public boolean IsEdge(int v, int w)

  Returns true if there is an edge between the vertices v and w in this SparseGraph instance.

• public void AddEdge(int v, int w)

  Add an edge connecting vertices v and w.

• public void RemoveEdge(int v, int w)

  Remove any edge connecting vertices v and w.

• public String toString()

  Return a String representing this instance. The String should consist of the contents each EdgeList (using the toString() instance method of that class) each list being separated by newline (i.e. "\n" characters).

What you should hand in

You should hand in to your Group Tutor:

1. A description of the exercise Requirements
2. Details of the design of your solution.
3. The source code for the SparseGraph class implementation.
4. Information regarding the test data and harness for your implementation:
   1. The design of the test harness.
   2. The data used to test the implementation.
   3. The output from your testing.

Notes

1. In constructing the test harness for your implementation you should ensure that each Constructor and each Instance method is tested.
2. You may find it helpful to use the int input methods to be found here. This provides a class method
   public static intget_int (BufferedReader instream )

   that will read a sequence of digits (stopping at a `whitespace' character) and return the integer value that has been read.

3. It is very easy to mis-type graph data (particularly if the graph has a large number of vertices), so you should try to prepare the test data in a separate file. For example, a 10 vertex graph could be

   
   0 1 1 0 1 1 0 1 1 0
   1 0 0 0 0 1 0 0 1 1
   1 0 0 1 0 1 0 0 0 1
   0 0 1 0 0 0 1 1 0 1
   1 0 0 0 0 1 0 0 0 0
   1 1 1 0 1 0 1 0 1 0
   0 0 0 1 0 1 0 0 0 0
   1 0 0 1 0 0 0 0 0 1
   1 1 0 0 0 1 0 0 0 1
   0 1 1 1 0 0 0 1 1 0
   
   

Your completed work should be handed in to your group tutor at your practical class on Thursday 24th February