10. Binary Trees and Tree Traversal

1. Introduction

One of the noticeable features common to the dynamic data structures that have been considered so far, is that they are all linear: each element within a structure can be accessed from at most one other element directly and provides access to at most one other element. An important form of dynamic ADTs providing for a much richer class of operations and algorithms are those whose organisation is non-linear in nature.

Among the most widely used of such forms is the class of Trees.

Here are two examples of information structures that might be modelled by trees:

Administrative Organisation,
e.g as In Figure 10.1 which illustrates (part) of the adminstrative structure governing the University of Liverpool,

Figure 10.1: A `Tree' structure modelling an administrative hierarchy.
Genealogical Trees.
As well the standard `family tree', one may have examples of these based on connections other than degrees of kinship. The example below show a fragment of a tree modelling Ph.D. research in areas related to Theoretical Computer Science, (a line connecting X to Y in this diagram indicates that X supervised Y's research; the information after any name refers to the university where research was undertaken and the year the Ph.D. was awarded).

Figure 10.2 A Genealogical Tree

These examples have several features in common:

There is a distinguished `parent' (or root) from which every other tree node is descended: in Figure 10.1 this is the node representing the whole University and the descendant nodes represent sub-structures within this; in Figure 10.2, it is the node associated with the mathematician H.A. Newton, all descendants are individuals whose Ph.D. work was overseen by a previous descendant or by Newton himself.
There is a unique path connecting the root node to any other node.
The sub-structures are themselves (smaller) trees, e.g. in Figure 10.1 we can view individual nodes representing Faculties as the parents (i.e. roots) of trees describing their adminstrative organisation.

In this lecture we consider a restricted type of tree structure and an implementation of this as a Java class: Binary Trees.

2. Binary Trees

The examples in Figure 10.1 and Figure 10.2 have the property that no limit has been imposed on the number of (direct) descendants (or children) a given node can have. The restriction that is used in the case of Binary Trees is that every node has at most two child nodes descending from it.

More formally,

Definition:

A Binary Tree, T is recursively defined as follows:

T is empty (i.e. contains no nodes).
OR
T consists of a root node which is connected to two distinct binary trees T_Left and T_Right
(`distinct' in the sense that T_Left and T_Right have no nodes in common).

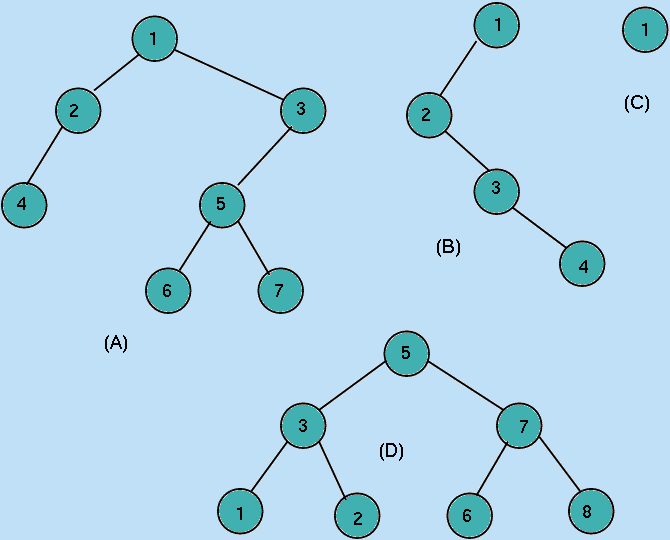
Thus, all of the examples in Figure 10.3 below are binary trees:

Figure 10.3: Examples of Binary Trees

The structure in Figure 10.3(A) has a root labelled 1, with the root of its Left sub-tree labelled 2 and its Right sub-tree labelled 3. In Figure 10.3(B), the Right sub-tree of the root is the empty tree, and in Figure 10.3(C), both sub-trees of the root are empty. The structure in Figure 10.4(D) is an example of what is sometimes called a complete binary tree: one which contains exactly 2^k-1 nodes where k is the number of nodes encountered on any path from the root to a lowest level node (i.e. one with no children).

The examples in Figure 10.4, however, are not binary trees

Figure 10.4: Examples of structures which are not Binary Trees

In Figure 10.4(A) and Figure 10.4(B) there are nodes with more than 2 children; Figure 10.4(C) is not a tree structure (in terms of our definition, the left and right sub-trees of the root can be viewed as not containing distinct sets of nodes).

It should be noted that Linked Lists can be seen as a special type of (Binary) tree, i.e. one in which every node has at most one child, and that Binary Trees (in fact Trees in general) can be viewed as a special type of Graph The latter viewpoint is useful when characterising properties shared by all trees. In this context (using the graph-theoretic terminology of Lecture 4, so that tree nodes are referred to as graph vertices, and links from parent to child nodes are referred to as graph edges), it is not difficult to show that all of the definitions below are equivalent:

Tree Properties

An n-vertex graph G(V,E) is a tree if:

There is a path of edges between any two vertices and there are exactly n-1 edges.
There is a path of edges between any two vertices and there are no cycles in G.
There is a unique path between any two vertices.

Tree Attributes

A leaf of a tree is a node that has no children.
The depth of a tree is the maximum number of nodes encountered on the unique path from the root to a leaf node.

Tree Properties and Attributes

Looking at the examples in Figures 10.1, 10.2, and 10.3:

The tree in Figure 10.1 has 10 nodes, 8 of which are leaves. Its depth is 3.
The tree in Figure 10.2 has 16 nodes, 6 of which are leaves. Its depth is 10.
The tree in Figure 10.3(A) has 7 nodes, 3 of which are leaves. Its depth is 4.
The tree in Figure 10.3(B) has 4 nodes, 1 of which is a leaf. Its depth is 4.
The tree in Figure 10.3(C) has 1 node which is a leaf. Its depth is 1.
The tree in Figure 10.3(D) has 8 nodes, 4 of which are leaves. Its depth is 3.

3. A Binary Tree Class in Java

In this part we consider the realisation of a basic Binary Tree class within Java. Later we shall develop this class in order to demonstrate how to maintain dynamically a collection of records that are sorted according to a given key, i.e. we present methods for adding and removing nodes from a binary tree so as always to be able consistently to output the records stored in the order required.

As will be clear using a binary tree structure to perform tasks such as that developed in Lecture 9, provides potentially very large saving in the time taken to maintain the record organisation.

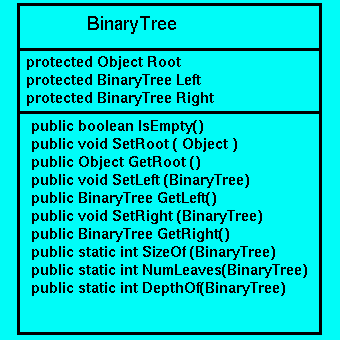
The recursive definition of a binary tree, motivates modelling a binary tree using three fields:

protected Object Root
protected BinaryTree Left
protected BinaryTree Right

We may use the default constructor in instantiating an instance of a BinaryTree and then simply require Instance methods with which to set and obtain the values of these fields. So, we have the Class diagram in Figure 10.5, in which three further static methods are, also, included:

Figure 10.5: BinaryTree Class Diagram.

The three Class Methods return the number of nodes (SizeOf(T)), number of leaves (NumLeaves(T)), and depth (DepthOf(T)), of the BinaryTree, T, given as a parameter. This class is realised as in Figure 10.6.


// COMP102
// Example 15: Binary Trees
//
// Paul E. Dunne 1/12/99
//
public class BinaryTree
  {
  protected Object Root;                 // Tree Root
  protected BinaryTree Left;             // Pointer to Left Sub-tree
  protected BinaryTree Right;            // Pointer to Right Sub-tree
  //*****************************************************
  // Binary Tree Methods                                *
  //*****************************************************
  //
  // Test is this tree contains no nodes
  //
  public boolean IsEmpty()
    {
    return (Root==null)&&(Left==null)&&(Right==null);
    }
  //*****************************************************
  // Set and Obtain the Root of this BinaryTree         *
  //*****************************************************
  public void SetRoot( Object root_val )
    {
    Root = root_val;
    }
  public Object GetRoot ()
    {
    return Root;
    }
  //*****************************************************
  // Set the Left/Right Subtress of this BinaryTree     *
  //*****************************************************
  public void SetLeft( BinaryTree L )
    {
    Left=L;
    }
  //
  public void SetRight( BinaryTree R )
    {
    Right=R;
    }
  //*****************************************************
  // Get the Left/Right Subtrees of this BinaryTree     *
  //*****************************************************
  public BinaryTree GetLeft ()
    {
    return Left;
    }
  //
  public BinaryTree GetRight()
    {
    return Right;
    }
   //*******************************************************//
   // Calculate the number of nodes in a given BinaryTree.  //
   //*******************************************************//
   public static int SizeOf( BinaryTree T )
     {
     if (T.IsEmpty())
       return 0;
     else
       return 1 + SizeOf(T.GetLeft()) + SizeOf(T.GetRight());
     }
   //*******************************************************//
   // Calculate the number of Leaves in a given BinaryTree*//
   //*******************************************************//
   public static int NumLeaves (BinaryTree T)
     {
     if (SizeOf(T) <= 1)
       return SizeOf(T);
     else
       return NumLeaves(T.GetLeft()) + NumLeaves(T.GetRight());
     }
   //*******************************************************//
   // Calculate the depth of nodes in a given BinaryTree.   //
   //*******************************************************//
   public static int DepthOf (BinaryTree T)
     {
     if (SizeOf(T) <= 1)
       return SizeOf(T);
     else
       return 1+Math.max( DepthOf(T.GetLeft()), DepthOf(T.GetRight()) );
     }
   }

Figure 10.6: BinaryTree Realisation.

4. Insertion, Deletion and Tree Traversal

One of the problems that is noticeable with LinkedLists as a dynamic ADT for maintaining a collection of records sorted according to some key field, is that as the collection increases in size, the typical time to search for a record with a given key can become excessive.

Using a binary tree organisation can significantly cut down this time. In this section we develop a set of methods, similar in spirit to those we considered in the application of Lecture 9, that can be employed to maintain a collection of records held within a binary tree structure.

Before describing these we need to consider what is understood by a data set being held in a `sorted order' within a binary tree: the concept of sorting and ordering is easily defined for the case of linear structures, such as linked lists or arrays, binary trees, however, are non-linear.

Recall that the BinaryTree class contains three fields: the Root with which arbitrary Objects may be referenced, and the Left, Right fields which are themselves BinaryTree instances. Suppose we have already defined (as was done in Lecture 9) a method

boolean IsBefore (Object X, Object Y)

that returns true if X precedes Y and X and Y are different.

Using this method and the approach outlined below, will not only allow a consistent definition of `sorted order' to be given for a BinaryTree object, but also ensure that a sequence of Objects can be formed into a `sorted' tree structure and recovered in a similar order.

Let,

X₁, X₂ ,. . ., X_i ,. . ., X_k

be a sequence of k instances of Objects (presumed to be of the same class). The algorithm InsertKey, maintains a BinaryTree instance, T, as follows:

public static void InsertKey (Object Key, BinaryTree T) { if (T is empty) // (This is only tree when the first Object (X₁) appears. { Set the Root of T to be the Object Key; Instantiate the Left and Right fields of T to be new BinaryTree instances. } else if (Key `is before' the Object held in the Root of T) { Recursively insert Key into the BinaryTree T.Left; } else if (Object held in the Root of T `is before' Key) { Recursively insert Key into the BinaryTree T.Right; }; }

A fuller realisation of this algorithm (in Java) is given later. We now enumerate the set of methods that will be used in maintaining a set of records held within a Binary Tree structure.
We utilise a class RecordTree to provide a set of static methods for manipulating BinaryTree instances. Its class diagram is given in Figure 10.7.

Figure 10.7: RecordTree Class Diagram.

Before we describe the purpose and realisation of these methods it is worthwhile to stress an extremely important shared feature of how many operations on binary tree structures may be realised.
The recursive definition of Binary Tree structure, provides a simple, natural, and extremely powerful basis for implementing all but the first two of the methods in the list. In essence binary tree methods can almost always be described in terms of the template in Figure 10.8, below:

If the tree is empty { do something and finish}
Carry out `some operation' on the Left sub-tree AND/OR
Carry out `some operation' on the Right sub-tree AND/OR
Process the Root of the tree.

Figure 10.8: General recursive framework for Binary Tree operations.

(where in the Left and Right sub-tree case, `some operation' will normally be a recursive invocation of the method realised).
For example, the static method SizeOf(BinaryTree T), calculate the number of nodes in a binary tree using,

If the tree is empty {its size is 0};
Calculate the number of nodes in the Left sub-tree; AND
Calculate the number of nodes in the Right sub-tree; AND
Add the two totals together with the number of nodes in the root (i.e. 1), returning the final total as result.

Returning to the RecordTree class, the functions provided by its methods are as follows:

public static boolean IsBeforeRoot ( Object Key, BinaryTree T )
Compare the Key Object with the Root Object field of the BinaryTree instance, T, returning true if Key precedes T.Root.

public static boolean IsAfterRoot ( Object Key, BinaryTree T )
Similarly, compare the Key Object with the Root Object field of the BinaryTree instance, T, returning true if Key succeeds T.Root.

public static boolean IsMemberOf( Object Key, BinaryTree T )
Test if the Key Object occurs in (i.e. is the Root field of T or one of its sub-trees) the BinaryTree T.

public static void InsertKey(Object Key, BinaryTree T)
Modify the BinaryTree T by inserting a node correspding to the Object Key into it. As with our LinkedList record scheme in Lecture 9, we do not allow the same Key to occur more than once in a given BinaryTree instance.

public static BinaryTree InsertTree(BinaryTree Add, BinaryTree T)
Similarly, insert the BinaryTree Add into T, again avoiding occurrences of duplicate keys.

public static BinaryTree DeleteKey(Object Key, BinaryTree T)
Return the structure of T resulting by removing the node corresponding to the Object Key. It is assumed that Key occurs at most once in T. If Key does not occur, then T itself is returned.

public static BinaryTree DeleteTree (Object Key, BinaryTree T)
Similarly, return the structure of T that results by removing the sub-tree whose Root corresponds the Object Key.

public static BinaryTree GetTree (Object Key, BinaryTree T)
Return the sub-tree of T whose Root corresponds to the Object Key. If Key does not occur in T, the empty tree is returned.

public static Object PreOrderFirst(BinaryTree T)
This and the following method will be dealt with later in the lecture.

public static Object PostOrderFirst(BinaryTree T)

In order to give an indication of how a typical recursively controlled binary tree method might be realised, we will concentrate on the 2 methods:

public static void InsertKey(Object Key, BinaryTree T)

public static BinaryTree DeleteKey(Object Key, BinaryTree T)
In realising the InsertKey method, the algorithm, given earlier is straightforward to implement in terms of the binary tree instance methods already described and the static methods of RecordTree, i.e.,

//*********************************************// // Insert a new Object into T, maintaining a *// // Sorted ordering *// //*********************************************// public static void InsertKey(Object Key, BinaryTree T) { if (T.IsEmpty()) { T.SetRoot(Key); T.SetLeft(new BinaryTree()); T.SetRight(new BinaryTree()); } else if ( IsBeforeRoot(Key,T) ) InsertKey(Key,T.GetLeft()); else if ( IsAfterRoot(Key,T) ) InsertKey(Key,T.GetRight()); }

Figure 10.9: Inserting a new Key into an ordered BinaryTree Instance

If we study this in terms of the `recursive template' of Figure 10.8: when the tree is empty, inserting a new Key into this produces a tree with a single node whose Root field is the Key and whose Left and Right sub-tree fields are empty BinaryTree instances; otherwise the Key is compared with the Object indicated by the Root field and recursively inserted into the approriate T.Left or T.Right trees. Notice that the realisation of the IsBefore(Object,Object) method ensures that duplication will be avoided.
The processes required for deleting a node ensuring that a correct ordering of the remaining nodes is maintained, is rather more complicated than the corresponding operation on LinkedList structures. The reason for this is that care must be taken not to eliminate the references to the Left and Right tree of the node that is being deleted.
Suppose we have identified the node of the tree that should be deleted, i.e. the one such that its Root field is equal to the Key.
There are three cases which are straightforward to deal with:

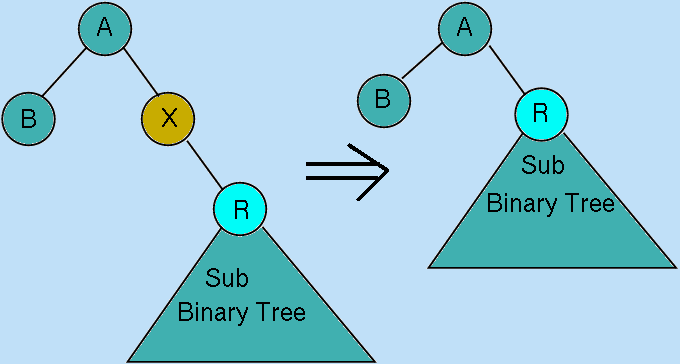
This node is a leaf: the Left and Right trees are empty, so the node can be replaced by a new empty BinaryTree instance.

Figure 10.10(a): Deleting Node X (X is a leaf)

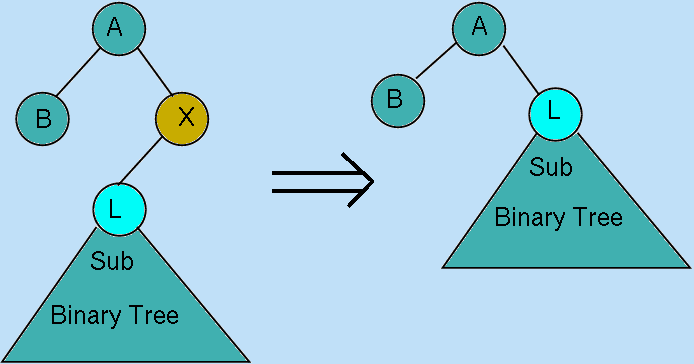
The Left sub-tree is an empty BinaryTree instance: the BinaryTree instance comprising the Right sub-tree can be returned as the result.

Figure 10.10(b): Deleting Node X (X has an empty Left sub-tree)

The Right sub-tree is an empty Binarytree instance: the BinaryTree instance comprising the Left sub-tree can be returned as the result.

Figure 10.10(c): Deleting Node X (X has an empty Right sub-tree)

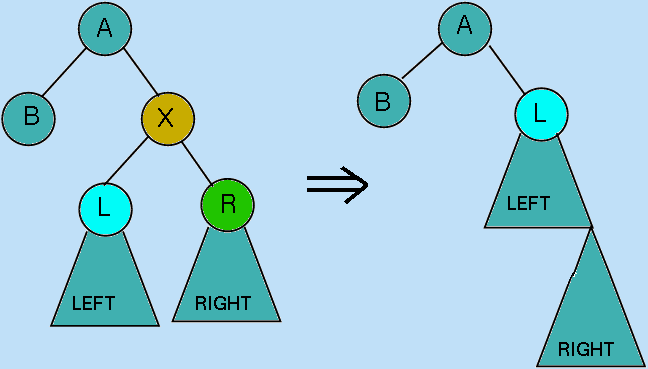
This leaves only the case where both sub-trees are not empty BinaryTree instances. What form should the replacement ordered tree take in this case?
From the ordering regime that has been employed it is known that every value held in the Left sub-tree PRECEDES every value held in the Right sub-tree, therefore if the BinaryTree formed by inserting the Right subtree into the Left subtree is constructed, this will be a correct structure with which to replace the BinaryTree instance whose Root field we wish to delete.

Figure 10.10(d): Deleting Node X (both sub-trees of X are non-empty)
In summary this gives the implementation of DeleteKey as in Figure 10.11:

//*******************************************************// // Return the BinaryTree that results by deleting // // the given Key from the tree structure. // //*******************************************************// public static BinaryTree DeleteKey(Object Key, BinaryTree T) { BinaryTree temp=new BinaryTree(); if ( !IsMemberOf(Key,T) ) return T; // Key not in T, so T is unchanged. else if (IsBeforeRoot(Key,T)) // Key is in T.Left, so delete recursively. { temp.SetRoot(T.GetRoot()); temp.SetRight(T.GetRight()); temp.SetLeft(DeleteKey(Key,T.GetLeft())); return temp; } else if (IsAfterRoot(Key,T)) // Key is in T.Right, delete recursively. { temp.SetRoot(T.GetRoot()); temp.SetLeft(T.GetLeft()); temp.SetRight( DeleteKey(Key,T.GetRight()) ); return temp; } // Key must be the current Root node; else if (BinaryTree.SizeOf(T)==1) { temp = new BinaryTree(); // If T has only one node, the empty tree remains return temp; // after deleting this. } else if (T.GetLeft().IsEmpty()) // If T.Left is empty, then after deleting T.Root, { temp = T.GetRight(); // the updated tree contains T.Right. return temp; } else if (T.GetRight().IsEmpty()) // If T.Right is empty, then after deleting T.Root, { temp = T.GetLeft(); // the updated tree contains T.Left. return temp; } else // By this stage: T.Root=Key and T.Left and { // and T.Right are both non-empty. //*********************************************************************** // The update `sorted' tree is built by inserting T.Right into the Tree * // Tree T.Left: this must preserve the correct `ordering' since every * // Object in T.Right must succeed every Object in T.Left. * //*********************************************************************** temp = InsertTree(T.GetRight(), InsertTree(T.GetLeft(), new BinaryTree())); return temp; }; }

Figure 10.11: Deleting a Key from an Ordered BinaryTree Instance

The complete implementation of the RecordTree class is presented in Figure 10.12.

// COMP102 // Example 16: Static Methods to Support Ordered Binary Trees // for Record Storage. // // Paul E. Dunne 2/12/99 // import BinaryTree; import Compare; public class RecordTree { //*******************************************************// // Compare the given key with the root of this Binary // // Tree, using a numeric comparison if both are Number // // instances, and String comparison otherwise. // // Returns true of Key is `less than' Root // //*******************************************************// public static boolean IsBeforeRoot ( Object Key, BinaryTree T ) { if (T.IsEmpty()) return false; else return Compare.IsBefore(Key,T.GetRoot()); } //*******************************************************// // Similarly, comparison method that returns true if *// // the given Key is 'greater than' the Root. *// //*******************************************************// public static boolean IsAfterRoot ( Object Key, BinaryTree T ) { if (T.IsEmpty()) return false; else return Compare.IsBefore(T.GetRoot(),Key); } //*******************************************************// // Test whether the given Key occurs as a node Object *// // in the BinaryTree T. *// //*******************************************************// public static boolean IsMemberOf( Object Key, BinaryTree T ) { if (T.IsEmpty()) return false; else if (IsBeforeRoot(Key,T)) return IsMemberOf(Key,T.GetLeft()); else if (IsAfterRoot(Key,T)) return IsMemberOf(Key,T.GetRight()); else return true; } //*********************************************// // Insert a new Object into T, maintaining a *// // Sorted ordering *// //*********************************************// public static void InsertKey(Object Key, BinaryTree T) { if (T.IsEmpty()) { T.SetRoot(Key); T.SetLeft(new BinaryTree()); T.SetRight(new BinaryTree()); } else if ( IsBeforeRoot(Key,T) ) InsertKey(Key,T.GetLeft()); else if ( IsAfterRoot(Key,T) ) InsertKey(Key,T.GetRight()); } //******************************************************// // Insert a SubTree Add into T, maintaining a *// // Sorted ordering (and avoiding item duplication) *// //******************************************************// public static BinaryTree InsertTree(BinaryTree Add, BinaryTree T) { BinaryTree temp = T; if (Add.IsEmpty()) return temp; else { InsertKey(Add.GetRoot(),temp); InsertTree(Add.GetLeft(),temp); InsertTree(Add.GetRight(),temp); return temp; }; } //*******************************************************// // Return the BinaryTree that results by deleting // // the given Key from the tree structure. // //*******************************************************// public static BinaryTree DeleteKey(Object Key, BinaryTree T) { BinaryTree temp=new BinaryTree(); if ( !IsMemberOf(Key,T) ) return T; // Key not in T, so T is unchanged. else if (IsBeforeRoot(Key,T)) // Key is in T.Left, so delete recursively. { temp.SetRoot(T.GetRoot()); temp.SetRight(T.GetRight()); temp.SetLeft(DeleteKey(Key,T.GetLeft())); return temp; } else if (IsAfterRoot(Key,T)) // Key is in T.Right, delete recursively. { temp.SetRoot(T.GetRoot()); temp.SetLeft(T.GetLeft()); temp.SetRight( DeleteKey(Key,T.GetRight()) ); return temp; } // Key must be the current Root node; else if (BinaryTree.SizeOf(T)==1) { temp = new BinaryTree(); // If T has only one node, the empty tree remains return temp; // after deleting this. } else if (T.GetLeft().IsEmpty()) // If T.Left is empty, then after deleting T.Root, { temp = T.GetRight(); // the updated tree contains T.Right. return temp; } else if (T.GetRight().IsEmpty()) // If T.Right is empty, then after deleting T.Root, { temp = T.GetLeft(); // the updated tree contains T.Left. return temp; } else // By this stage: T.Root=Key and T.Left and { // and T.Right are both non-empty. //*********************************************************************** // The update `sorted' tree is built by inserting T.Right into the Tree * // Tree T.Left: this must preserve the correct `ordering' since every * // Object in T.Right must succeed every Object in T.Left. * //*********************************************************************** temp = InsertTree(T.GetRight(), InsertTree(T.GetLeft(), new BinaryTree())); return temp; }; } //************************************************* // Delete sub-tree with root Key from T * //************************************************* public static BinaryTree DeleteTree (Object Key, BinaryTree T) { BinaryTree temp=new BinaryTree(); if (!IsMemberOf(Key,T)) { temp=T; return temp; } else if (IsBeforeRoot(Key,T)) { temp.SetRoot(T.GetRoot()); temp.SetRight(T.GetRight()); temp.SetLeft(DeleteTree(Key,T.GetLeft())); return temp; } else if (IsAfterRoot(Key,T)) { temp.SetRoot(T.GetRoot()); temp.SetLeft(T.GetLeft()); temp.SetRight(DeleteTree(Key,T.GetRight())); return temp; } else return temp; // Key=T.Root, so deleting T.Root leaves the empty tree. } //************************************************* // Return the BinaryTree whose sub-tree has its * // Root field equal to Key. * // If Key does not occur in T returns the empty * // BinaryTree. * //************************************************* public static BinaryTree GetTree (Object Key, BinaryTree T) { BinaryTree result; if (!IsMemberOf(Key,T)) result=new BinaryTree(); else if (IsBeforeRoot(Key,T)) // Key in T.Left result = GetTree(Key,T.GetLeft()); else if (IsAfterRoot(Key,T)) // Key in T.Right result = GetTree(Key,T.GetRight()); else result = T; // Key=T.Root return result; } //************************************************* // Return the Object which occurs first in a * // InOrder traversal: i.e. the `first' Object * // in the tree ordering. * // Error will be raised if T is empty. * //************************************************* public static Object InOrderFirst(BinaryTree T) { if (T.GetLeft().IsEmpty()) return T.GetRoot(); else return InOrderFirst(T.GetLeft()); } //************************************************* // Return the Object which occurs first in a * // PostOrder traversal: i.e. the `last' Object * // in the tree ordering. * // Error will be raised if T is empty. * //************************************************* public static Object PostOrderFirst(BinaryTree T) { if (T.GetLeft().IsEmpty()) { if (T.GetRight().IsEmpty()) return T.GetRoot(); else return PostOrderFirst(T.GetRight()); } else return PostOrderFirst(T.GetLeft()); }

Figure 10.12: Maintaining a Sorted Record Structure in a BinaryTree

4.1. Binary Tree Traversal

There are two methods mentioned in our RecordTree class that we have deferred a discussion of: the methods,

public static Object PreOrderFirst(BinaryTree T)

public static Object PostOrderFirst(BinaryTree T)
Given that one of the aims of the RecordTree class is to aid in maintaining an ordered collection of records using a BinaryTree, it would be desirable to have methods to output the contents of the Root fields to demonstrate both the `first-to-last' and 'last-to-first' ordering. In addition, it is frequently useful (e.g. as in the implementation of the InsertTree method) to recover an ordering that would yield exactly the same tree structure were the sequence of Object instances returned to be formed into an ordered BinaryTree.
Techniques for processing the nodes of a (binary) tree according to some ordering protocol, are called

Tree Traversal Methods
Each of the the three ordering mechanisms mentioned can be recovered by traversal methods known as:

IN-ORDER Traversal.
PRE-ORDER Traversal.
POST-ORDER Traversal.

In-order traversal, is use to process individual keys stored in the tree respecting the `first-to-last' sorted order.
Pre-order traversal, is use to process individual keys stored in the tree respecting the exact structure of the tree.

Recalling that there are exactly 3 fields defining a BinaryTree instance - Left, Root, Right, consider the following possible schemes for processing these:

Recursively traverse the Left sub-tree; process the Root; recursively traverse the Right sub-tree.
Process the Root; recursively traverse the Left sub-tree; recursively traverse the Right sub-tree.
Recursively traverse the Left sub-tree; recursively traverse Right sub-tree; process the Root.

It is not difficult to see that the first of these (called In-Order) reproduces the sorted ordering; the second (called Pre-Order) and the final method is called Post-Order).
A set of graphical animations, illustrating these different approaches, can be accessed from this page. You should read the warning notes with care before loading the relevant animations.

5. Summary

Binary Tree structures provide an alternative solution to the problems of dynamic maintainance of collections of information.
The main advantages offered by tree mechanisms is that, if properly structured, access to specific records will typically be significantly faster than the use of a linked list structure. Thus, it would appear that for very large collections binary tree organisation is more suitable.
The standard operations on Binary trees (inserting a key, searching for a key, traversal), illustrate one of the fundamental control mechanisms in the design of algorithms: that of recursion. Many ADTs may most naturally be specified using a recursive definition (e.g. Lists as we saw earlier). When such is the case, it is likely that standard operations on these may be very easy to realise by devising a recursive algorithm. Binary trees provide on the the best examples of such an approach.
Imposing an ordered structure to govern maintenance of a set of records within a binary tree can, however, create problems when compared to lists. Not only is the delete operation considerably more complicated than that for linked lists, there is also the problem that over a large number of deletions the tree becomes highly `unbalanced', thus increasing the time it may take to search for a record. For this reason, a pure binary tree realisation may turn out to be less effective than a linked list if the collection of records varies significantly over a period of time.
Finally, the initial structure created for a binary tree is very dependent on the order in which keys are added: in the worst-cases (keys arrive in sorted order or reverse order), the organisation will in fact be identical to a linked list structure. In more sophisticated realisations methods may be used to detect when a tree has become `too unbalanced' and re-organise it to improve things. Such methods, however, may incur a prohibitive time penalty.

(Notes prepared and maintained by Paul E. Dunne, December 1999)