 |
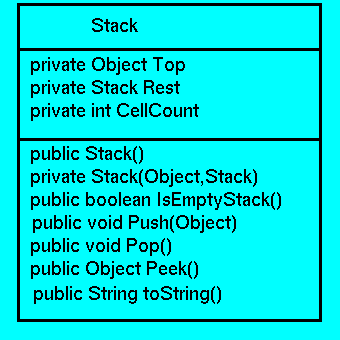
Figure 7.1: Class Diagram for a Stack Object.
The LinkedList class that was presented in Lecture 6, provides a general mechanism implementing a dynamically adaptable structure. In Lecture 9 we will demonstrate how this basic structure can be adapted to allow
There are many applications, however, for which it is useful to impose a strict regime governing the order in which data held in a structure can be accessed. Examples of such regimes are:
then such a regime would provide access to Item A (which when removed would leave Item B::Item C) and Item C (which when removed would leave Item A :: Item B), but not (immediate) access to Item B (one of the surrounding items would first have to be removed).
Notice that the form prescribed by the LIFO regime, has been realised by the LinkedList class. There are, however, many other mechanisms which could have been used to the same effect.
The ADTs used to hold data so that access to these is controlled by the different protocols described have specific names associated with them in a Computer Science context.
Several of you will already have met Stack structures in the context of low-level programming on the module COMP103.
In this lecture we consider the standard set of operations associated with Stacks, examine their realisation in Java, and analyse an example application using them. Queue structures will be considered in the next lecture.
The Stack ADT is a frequently used structure particularly within the realisation of systems software programs, e.g. High-level language compilers and Operating Systems. Typical applications of Stacks in the former instance are:
public static int factorial ( final int n )
{
if (n==1)
return 1;
else
return n*factorial(n-1);
}
|
The parameter n referenced when this method is called is `different' on successive
recursive calls. The usual technique that is employed in compilers in order to `keep track'
of the `correct' reference, is to place (push) the (reference to) the `new' location of
n for a given recursive call onto a stack. This can be emptied (or
popped) once the terminating condition (n==1) has
been reached.
Figure 7.1, below presents a Java Class Diagram for a Stack Object. In naming the methods used, we have adhered to the conventional names by which these are usually referred in the literature and applications programs.
 |
Figure 7.1: Class Diagram for a Stack Object.
Notice there is a similarity to the ListCell class that we considered in Lecture 5: the fields of a Stack instance are:
The first two of these play a role similar to that of the fields Datum and Link defined for the ListCell class.
Of the two constructors, only one of these
is available for use by applications employing the Stack class. The other one,
is only available to be used internally within Instance methods of the class. The implementation of this constructor is, again, similar to the corresponding constructor within the ListCell class.
By using 2 constructors, one of which is hidden, we save nesting the ListCell class details within the Stack class realisation, while continuing to avoid the drawbacks that led to this being done for our LinkedList realisation of Lecture 6.
Of the 5 instance methods, the important operations on a Stack are
which returns true if and only if this Stack contains no data Objects.
which places a new Object, T, onto the top of this Stack.
which removes the Object at the top of this Stack.
which returns the Object at the top of this Stack, but without altering the Stack contents.
The full implementation of the Stack class is given in Figure 7.2., below
//
// COMP102
// Example 10: Stacks
//
//
// Paul E. Dunne 11/11/99
//
public class Stack
{
//******************************************************
// Stack Fields *
//******************************************************
private Object Top;
private Stack Rest;
private int CellCount;
//******************************************************
// Stack Constructors *
//******************************************************
public Stack()
{
Top = null;
Rest = null;
CellCount=0; // Initiates the empty Stack
}
//***************************************************************
// This constructor is private, and is used to ensure that *
// the correct sequence of pointers is set up for this instance *
//***************************************************************
private Stack( Object Item, Stack rest_of )
{
Top = Item;
Rest = rest_of;
}
//******************************************************
// Stack Instance Methods *
//******************************************************
//
// Test if this instance is the Empty Stack.
//
public boolean IsEmptyStack()
{
return (CellCount==0);
};
//
//************************************************************
// Add a new Cell as the first cell in this Stack *
//************************************************************
//
public void Push ( Object Datum )
{
if (IsEmptyStack())
{
Top =Datum;
Rest = null;
}
else
{
Rest = new Stack (Top,Rest); // N.B. Use of private Constructor here;
// compare with ListCell Constructor earlier.
Top = Datum;
};
this.CellCount++;
}
//
//************************************************************************
// Remove the Cell at the top of this Stack. *
// i.e. if the current Stack is [Top]::[Rest], the `new' one is [Rest]. *
//************************************************************************
//
public void Pop()
{
if (CellCount<=1) // There is an argument for raising
{ // an exception if CellCount=0
// however, we adopt the convention
// that Pop() applied to
// the empty Stack leaves the empty Stack.
Top = null;
Rest=null;
CellCount=0;
}
else
{
Top = Rest.Top;
CellCount--; // and this Stack has one fewer cell.
if (CellCount==1)
Rest=null; // If there's only a single cell then its Rest field
// must point to the empty Stack (i.e. null reference)
else
Rest = Rest.Rest; // Otherwise we can update Rest without any problem.
};
}
//
//**********************************************************************
// Obtain the Object in the Top field of this Stack *
// This method will not change the current instantiation. *
//**********************************************************************
//
public Object Peek()
{
if (!(CellCount==0)) // If there's anything to return
return this.Top; // then return it.
else
return null; // otherwise return a null reference.
}
//
//******************************************************
// Convert this Stack to a String suitable for output. *
//******************************************************
//
public String toString()
{
String res = new String();
Stack temporary = new Stack();
temporary.Top = this.Top;
temporary.Rest = this.Rest;
temporary.CellCount=this.CellCount;
while (!temporary.IsEmptyStack())
{
res = res+(temporary.Peek()).toString()+"\n";
temporary.Pop();
};
return res;
}
}
|
Figure 7.2: Implementation of a Stack Class in Java
Earlier we mentioned a standard application of Stacks, arising in the context of High-level Language Compilers, was to generate appropriate low-level code to evaluate an arithmetic expression given in the form of Reverse Polish Notation (RPN) (also called, for reasons that will become obvious, Postfix Notation).
As an example of using the Stack class, we develop a Java program that will take as input an arithmetic expression in RPN (involving non-negative integer constants and the arithmetic operations +, -, *, /) and output the integer value to which this expression corresponds.
Before giving a more complete description of the requirements, we first give a precise definition of what constitutes an Integer valued Reverse Polish expression.
|
An Integer value arithmetic expression, E is in Reverse Polish Form if:
|
|
If E is an integer arithmetic expression in Reverse Polish Form, its
arithmetic value, V(E), is
|
Reverse Polish Form for Integer Arithmetic Expressions
For example, the following are all expressions in Reverse Polish Form:
| Example | Expression | Form (1) or (2) | Value |
| 1 | 25 | (1), Constant | 25 |
| 2 | 0 5 - | (2) E1=0; E2=5; opn=- | -5 = 0-5 |
| 3 | 25 0 5 - / | (2) E1=(Ex1); E2=(Ex2); opn=/ | -5 = V( Ex1 )/V(Ex2) |
| 4 | 25 0 5 - / 10 + | (2) E1=(Ex3); E2=10; opn=+ | 5 = V(Ex3) + 10 |
Figure 7.3 Some Simple Examples of Reverse Polish Notation and their Evaluation.
We can now give a fuller description of the,
Given a sequence, S, of input data comprising non-negative integer values and arithmetic operations, terminated by the character @, print out the integer value V(S) if S is a correctly formed integer arithmetic expression in Reverse Polish Notation; if S is not a correctly formed expression in Reverse Polish Notation output an error message.
It may be assumed that all constant values occurring in S are non-negative integers (i.e. there are no floating point values).
Consider the recursive definition given earlier of the value of an expression in Reverse Polish. This definition indicates that the value of
could be found be finding the operation at the end of the expression, (this would be the symbol preceding the @ sign in the requirements description) and then applying this to the value of the two preceding expressions. With a typical input S, however, being a sequence of integer values and operators, how do we find out where E1 ends? The answer is that it is not necessary to know this. All we have to notice is that any well-formed RPN (if it's not a constant value) must end with an operator symbol. So consider the following `informal' algorithm for processing S:
Suppose
where each wi is either an integer constant or an operator symbol:
Thus this approach performs a calculation every time an operator
is found in the input data. Furthermore, the operation is carried out on the two most recently
saved constant values. In other words, the ordering regime is such that the last integer
constant `saved' will be the first one to be used when an operator is found.
This suggests realising steps (2) and (3) by using a stack as the structure on which
to `save' values.
The fields required in the main() method, are given with a description below:
The natural control mechanism structure suggested by the requirements is that of
a while loop, during the running of which input data is
read and processed, i.e.
Since there are several different ways in which a badly-formed Reverse Polish Expression could
arise, we use a boolean `flag' which is set to true
when an error is discovered.
In addition, since a single character ('@') is used to indicate the end of an expression,
the natural input mechanism is to read data one character at a time from the input stream.
So we will add the following variables to those in the main() method.
So that the loop condition becomes,
The input (from a keyboard or prepared file) characters can be classified into 5 distinct groups:
Any input character in the last group cannot be part of a well-formed expression, so if such
are detected the error_flag can be set to true.
The action required when the termination symbol is read has already been described.
What about the remaining character groups?
Obviously, we want to ignore any characters that belong to the `white space' category, and
so arrange that the next_ch variable will only result in one of the other four
categories requiring action to be taken in processing the expression. In order to facilitate
this, the method in Figure 7.4 is used.
Figure 7.4: Method to return the next non `white space' char in the input.
This is invoked to set the initial value of next_ch prior to the main while
loop being entered.
This leaves us with the first two groups which are the cases that one would expect
to predominate in a typical input.
In order to recognise whether the character in next_ch is one of the operator
symbols, we can use a method that performs a simple test on a character parameter, i.e
Of course there are further actions required in this case (as there are if we find that
the character is a digit).
The framework we have so far is:
Process Digit Case
A digit indicates that item to be read is an integer constant value. In this case it is necessary
to
Figure 7.5 Realisation of the steps required when next_ch is a digit.
Process Operator Symbol Case
Following the algorithm outlined earlier
when next_ch indicates an operator symbol, the following action
is required
If there are fewer than two items on the RPN_Expr Stack
then it must be the case that the expression was not properly formed RPN, in which
event the error_flag can be set.
Figure 7.6: Stack Processing when Operator Symbol Occurs.
The final stage is to output the value remaining on the RPN_Expr
Stack when the loop is exited, checking that
exactly one value remains on the Stack.
The full realisation of the algorithm is given in Figure 7.7.
Figure 7.7: Complete Implementation of Reverse Polish Evaluator using Stack Class.
1. i=1 2. if wi is an integer constant then `save' its value `somewhere' 3. if wi is an operator then `replace' the `last' value saved with the result of applying the operator to the 'last' two values saved. 4. i = i+1 5. Go to Step 2. if i<=m
Stack RPN_Expr; // The expression being evaluated.
Integer Operand= new Integer(0); // Object sub-class to use when
// placing integer values on Stack.
// N.B. Wrapper class.
int ValueLeft,ValueRight; // Used during evaluation of expression in
// the form Left Right <opn>, so that
// ValueLeft == V(Left);
// ValueRight == V(Right);
int FinalValue=0; // For the expression result.
String temp; // Will hold integer values under construction
while ( termination symbol not read && no errors found in expression )
{
Continue processing input data
};
while ( !( (next_ch=='@')||(error_flag) ))
{
Continue processing input data
};
//*******************************************************
// Strip out spaces and newlines between input items *
// Return the first `non white space' char found. *
//*******************************************************
public static char IgnoreWhiteSpace( BufferedReader instream)
throws IOException
{
char c=' ';
while (Character.isWhitespace(c))
{
c = (char)instream.read();
};
return c;
}
//***************************************************************
// Check if the character just read is an arithmetic operation *
//***************************************************************
public static boolean OperatorSymbol( char c )
{
return ( (c=='+')||(c=='-')||(c=='*')||(c=='/') );
}
next_ch = IgnoreWhiteSpace(keyboardInput); // Find first
// `real' input char.
while (!( (next_ch=='@')||(error_flag) ))
{
if Character.IsDigit (next_ch)
Process digit case
else if OperatorSymbol(next_ch)
Process Operator case
else
error_flag = true
}
...
That is,
temp = new String();
//
//********************************************
// If next item is an integer value; *
// then it will start with a digit. *
//********************************************
//
if (Character.isDigit(next_ch))
{
//*************************************************
// and end at the character immediately preceding *
// the next non-digit character read. *
//*************************************************
while (Character.isDigit(next_ch))
{
temp = temp+next_ch;
next_ch = (char)keyboardInput.read();
};
Operand = new Integer(temp);
RPN_Expr.Push(Operand); // Put the value just read onto the Stack.
//********************************************************************
// The non-digit character might be a space, or linebreak *
// If it is, we want the next character inspected to be a digit *
// or operation and so we have to get rid of intermediate 'noise' *
// characters (spaces, linebreaks, etc.). *
//********************************************************************
if (Character.isWhitespace(next_ch))
next_ch = IgnoreWhiteSpace(keyboardInput);
}
//********************************************************************
// If the character is an operator then the top 2 items *
// currently on the Stack, (V1, V2 say) can be replaced by *
// the integer value V1 <op> V2. *
//********************************************************************
else if (OperatorSymbol(next_ch))
{
//*****************************************************************
// If the input expression is in a correct form then there *
// must be (at least) 2 values on the Stack at this point. *
//*****************************************************************
if (RPN_Expr.IsEmptyStack())
error_flag = true;
else
{
//*************************************************
// Find out the value of the `right-hand' operand.*
//*************************************************
ValueRight = (Integer.valueOf(RPN_Expr.Peek().toString())).intValue();
RPN_Expr.Pop(); // and remove it from the Stack.
//********************************************************************
// Make sure that there's at least one value remaining on the Stack. *
//********************************************************************
if (RPN_Expr.IsEmptyStack())
error_flag=true;
else
{
//*************************************************
// Find out the value of the `left-hand' operand. *
//*************************************************
ValueLeft = (Integer.valueOf(RPN_Expr.Peek().toString())).intValue();
RPN_Expr.Pop(); // and remove this from the Stack,
switch (next_ch) // Now compute what should replace these values.
{
case '+': Operand = new Integer(ValueLeft+ValueRight);
break;
case '-': Operand = new Integer(ValueLeft-ValueRight);
break;
case '*': Operand = new Integer(ValueLeft*ValueRight);
break;
case '/': Operand = new Integer(ValueLeft/ValueRight);
};
RPN_Expr.Push(Operand); // and save it onto the Stack.
next_ch = IgnoreWhiteSpace(keyboardInput); // Continue with the
// next character.
};
};
}
//
// COMP102
// Example 11: Evaluation of Arithmetic Expressions
// in Reverse Polish Notation Using
// the Stack class.
//
// Paul E. Dunne 15/11/99
//
import java.io.*;
import Stack;
public class RPN
{
public static InputStreamReader input = new InputStreamReader(System.in);
public static BufferedReader keyboardInput = new BufferedReader(input);
//*******************************************************
// Strip out spaces and newlines between input items *
// Return the first `non white space' char found. *
//*******************************************************
public static char IgnoreWhiteSpace( BufferedReader instream)
throws IOException
{
char c=' ';
while (Character.isWhitespace(c))
{
c = (char)instream.read();
};
return c;
}
//***************************************************************
// Check if the character just read is an arithmetic operation *
//***************************************************************
public static boolean OperatorSymbol( char c )
{
return ( (c=='+')||(c=='-')||(c=='*')||(c=='/') );
}
//***************************************************************
// Main method *
//***************************************************************
public static void main( String[] args) throws IOException
{
Stack RPN_Expr; // The expression being evaluated.
Integer Operand= new Integer(0); // Object sub-class to use when
// placing integer values on Stack.
// N.B. Wrapper class.
int ValueLeft,ValueRight; // Used during evaluation of expression
// in the form Left Right <opn>,
// so that ValueLeft == V(Left);
// ValueRight == V(Right);
int FinalValue=0; // For the expression result.
char next_ch; // Characters read from input stream.
boolean error_flag = false; // Set to true if invalid expression.
String temp; // Will hold integer values.
String Clearout; // Remove anything left on input line,
// before prompting for continuation.
char YesNo='N'; // To indicate whether to continue.
//***********************************************************************
System.out.println("Enter arithmetic expression in Reverse Polish Form");
System.out.println("use '@' symbol to end expression");
next_ch = IgnoreWhiteSpace(keyboardInput); // Find first `real' input.
RPN_Expr = new Stack();
//
//***************************************************************
// Continue evaluation until end of expression marker reached *
// or an error has been found in the expression input form. *
//***************************************************************
//
while (!( (next_ch=='@')||(error_flag) ))
{
temp = new String();
//
//********************************************
// If next item is an integer value; *
// then it will start with a digit. *
//********************************************
//
if (Character.isDigit(next_ch))
{
//*************************************************
// and end at the character immediately preceding *
// the next non-digit character read. *
//*************************************************
while (Character.isDigit(next_ch))
{
temp = temp+next_ch;
next_ch = (char)keyboardInput.read();
};
Operand = new Integer(temp);
RPN_Expr.Push(Operand); // Put the value just read onto the Stack.
//********************************************************************
// The non-digit character might be a space, or linebreak *
// If it is, we want the next character inspected to be a digit *
// or operation and so we have to get rid of intermediate 'noise' *
// characters (spaces, linebreaks, etc.). *
//********************************************************************
if (Character.isWhitespace(next_ch))
next_ch = IgnoreWhiteSpace(keyboardInput);
}
//********************************************************************
// next_ch cannot be a whitespace character. If it's not a digit *
// it should be an operator symbol (or the terminal '@' symbol). *
//********************************************************************
// If the character is an operator then the top 2 items *
// currently on the Stack, (V1, V2 say) can be replaced by *
// the integer value V1 <op> V2. *
//********************************************************************
else if (OperatorSymbol(next_ch))
{
//*****************************************************************
// If the input expression is in a correct form then there *
// must be (at least) 2 values on the Stack at this point. *
//*****************************************************************
if (RPN_Expr.IsEmptyStack())
error_flag = true;
else
{
//*************************************************
// Find out the value of the `right-hand' operand.*
//*************************************************
ValueRight =
(Integer.valueOf(RPN_Expr.Peek().toString())).intValue();
RPN_Expr.Pop(); // and remove it from the Stack.
//***************************************************************
// Make sure there's at least one value remaining on the Stack. *
//***************************************************************
if (RPN_Expr.IsEmptyStack())
error_flag=true;
else
{
//*************************************************
// Find out the value of the `left-hand' operand. *
//*************************************************
ValueLeft =
(Integer.valueOf(RPN_Expr.Peek().toString())).intValue();
RPN_Expr.Pop(); // and remove this from the Stack,
switch (next_ch) // Compute what should replace these.
{
case '+': Operand = new Integer(ValueLeft+ValueRight);
break;
case '-': Operand = new Integer(ValueLeft-ValueRight);
break;
case '*': Operand = new Integer(ValueLeft*ValueRight);
break;
case '/': Operand = new Integer(ValueLeft/ValueRight);
};
RPN_Expr.Push(Operand); // and save it onto the Stack.
next_ch = IgnoreWhiteSpace(keyboardInput); // Continue with the
// next character.
};
};
}
//**************************************************************
// The character read cannot be the terminating '@' symbol so *
// if it was not a digit, and not an operator symbol, then the *
// input expression is not in correct RPN. *
// In this case, we can set the error flag to true and exit. *
//**************************************************************
else
error_flag = true;
};
//*******************************************************
// On completion, there should be exactly one value on *
// the Stack. *
//*******************************************************
if (RPN_Expr.IsEmptyStack())
error_flag=true;
else
{
FinalValue =
(Integer.valueOf(RPN_Expr.Peek().toString())).intValue();
RPN_Expr.Pop();
};
//***********************************
// Now the Stack should be empty. *
//***********************************
if (!(RPN_Expr.IsEmptyStack()))
error_flag=true;
//
if (error_flag)
System.out.println
("Expression is not in correct Reverse Polish Notation");
else
System.out.println("The value of this expression is "+ FinalValue);
System.out.println();
Clearout = keyboardInput.readLine(); // Get rid of any noise.
System.out.print("Continue with another expression? (Y/y):");
YesNo = (keyboardInput.readLine()).charAt(0);
if ((YesNo=='Y')||(YesNo=='y'))
main(args); // Clumsy way of iterating,
// but easiest solution.
}
}
The test conditions are summarised below:
| Input | Expected outcome | Actual Outcome |
| @ | Incorrect RPN expression | Incorrect RPN |
| +@ | Incorrect RPN expression | Incorrect RPN |
| 25@ | 25 | 25 |
| 'white space'@ | Incorrect RPN expression | Incorrect RPN |
| 25'white space'@ | 25 | 25 |
| 'white space'25'white space'@ | 25 | 25 |
Figure 7.8: Limit Test Results for RPN Application.
| Input | Expected outcome | Actual Outcome |
| 3 4 +@ | 7 | 7 |
| 3 4 -@ | -1 | -1 |
| 3 4 *@ | 12 | 12 |
| 3 4 /@ | 0 | 0 |
| 3 +@ | Incorrect RPN | Incorrect RPN |
| 3 4 + 5 6 *@ | Incorrect RPN | Incorrect RPN |
| 3 4 + 5 6 * +@ | 37 | 37 |
| 1 2 3 4 5 6 7 8 9 ++++++++@ | 45 | 45 |
Figure 7.9: Path Testing Results for RPN Application.