 |
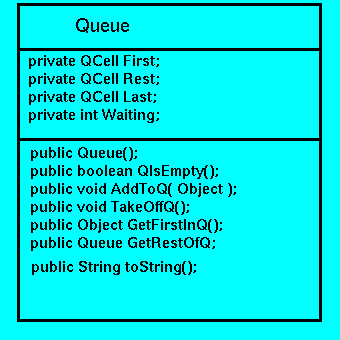
Figure 8.1: Queue Class Diagram
The Stack Class whose realisation was presented in the previous lecture organises data using a LIFO, i.e. Last-In-First-Out, regime. As we saw with the example of evaluating expression given in Reverse Polish Notation, such regimes offer a natural ADT for some applications problems.
An ordering regime which is more familiar in practice, however, is that of a Queue, which uses a FIFO, i.e. First-In-First-Out, regime.
Queues are a familiar structure in everyday situations, e.g.
One may also identify many simple examples of queuing structures within the specific area of Computer Systems, e.g.
From such examples it is clear that Queues may arise in applications either directly as a natural protocol to use in prioritising requests for a specific task to be carried out, or in modelling `real-world' scenarios (such as the two mentioned) within simulation systems.
In this lecture we present a possible realisation of a Queue
ADT in Java, using as a basis the ListCell Object
that was introduced in Lecture 5.
The Class Diagram for the Queue Class is shown in Figure 8.1.
 |
Figure 8.1: Queue Class Diagram
Notice that the fields, First, Rest, and Last in the Queue class are specified as having type QCell. This class, which will be accessible only within the methods and constructor for the Queue class, plays a similar role to that of the ListCell class that we have been using. The Class diagram for the QCell Class is presented in Figure 8.2.
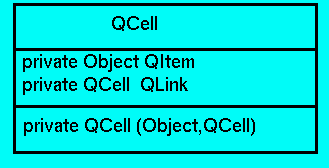 |
Figure 8.2: QCell Class Diagram.
The field QItem of a QCell instance will indicate the Object that is associated with this part of the Queue. The QLink field points to the QCell that immediately folows it in this Queue. Thus a Queue is viewed as a linked sequence of instances of QCell. The sole constructor, which can only be accessed from within the methods of the Queue class, for QCell, instantiates the QItem field to the Object given as a parameter and the QLink field to the QCell specified, i.e.
private class QCell
{
//
// QCell Fields
//
private Object QItem;
private QCell QLink;
//
// QCell Constructor
//
private QCell(Object head, QCell NextInQ)
{
QItem = head; QLink=NextInQ;
}
}
|
Figure 8.3: Implementation of the private QCell Class.
Returning to the realisation of the Queue class itself, we can examine how instances of QCell are used.
The Queue class comprises 4 fields:
This field represents the item at the start of this Queue: thus the field First.QItem indicates the head of this Queue, the field First.QLink indicates items that follow it (if any).
The items in this Queue that are after the first item. An invariant property of the implementation is that First.QLink and Rest always indicate the same QCell.
The field Last.QItem this indicates the most recently added Object to be placed on this Queue. The field Last.QLink will always be the null reference, however, when an instance of a new QCell, newLast say, is added then (the current) Last.QLink will change to indicate the QCell newLast, and the Last field updated to point at newLast.
This will keep a count of the number of items held in this Queue.
The single constructor, Queue(), instantiates these fields to represent the empty Queue, i.e. with the three QCell fields set to the null reference, and the Waiting counter initiated to 0.
The 6 methods defined fulfil the following roles.
Returns true if this Queue is empty, i.e. Waiting==0.
Form a new QCell whose QItem field is set to the Object EndOfQ. This QCell is then added to this Queue as its (new) Last field.
Changes this Queue by removing its First QCell. First is then updated to reference First.QLink.
Return the Object First.QItem of this Queue, without altering the queue structure.
Similarly, returns the Queue indicated by the First.QLink, again without altering the structure of this Queue.
Converts this Queue into a String, in which the associated queue items appear in the order given by the queue structure.
With the exceptions of the second and third methods
the implementation of these is substantially the same as the related methods given earlier (under different names) in the LinkedList and Stack implementations.
In the case of Queues, however, we have to take into consideration the different ordering protocol that pertains to these.
In the AddtoQ method, the Object being added must be placed at the end of the queue, i.e. the Last item will become the Object being added to this instance. Figure 8.4, gives the implementation of the AddtoQ method:
//************************************************************
// Add a new Object to the end of this Queue; *
// The new item is added in such a way that in traversing *
// this Queue, the item will be the Last one found. Further *
// additions will be appended after this. *
//************************************************************
public void AddToQ ( Object EndofQ )
{
QCell temp;
//**********************************************************
// If this Queue is empty then the First and Last Queue *
// Cells are identical. *
//**********************************************************
if (QIsEmpty())
{
Last = new QCell(EndofQ,Last);
First = Last;
Rest = First.QLink;;
Waiting=1;
}
else
{
Last.QLink = new QCell(EndofQ,Last.QLink); // The last item is the one being added.
Last = Last.QLink;
Waiting++; // Increase Length of this Queue.
};
}
|
Figure 8.4: The Method for Adding an item at the end of a Queue.
Notice that the case of adding an item to an empty queue must be treated separately, since in this case the First and Last fields must indicate the same QCell instance.
Similarly, when the item at the head of a queue is removed, it is necessary to take care that the field First is updated correcly. The method, TakeOffQ, that deals with this is shown in Figure 8.5.
public void TakeOffQ()
{
if (Waiting<=1) // Will leave the empty Queue
{ // after removal.
First = null; Last=null; Rest=null;
Waiting=0;
}
else
{
First = First.QLink; // Find the `new' head of the Queue.
Waiting--; // One fewer item in Queue.
if (Waiting==1) // Deal with the case that there's
{ // exactly one item left in this Queue.
Last = First;
Rest = null;
}
else
Rest = First.QLink; // If more than one; reset Rest of Queue
}; // indicator.
}
|
Figure 8.5: The method to remove the item at the head of a queue.
Again we use the convention that the result of applying this method to an empty queue will leave the empty queue, i.e. the null reference exception is avoided.
The complete implementation of the Queue class is given in Figure 8.6 below.
//
// COMP102
// Example 12: Queues
//
// Paul E. Dunne 20/11/99
//
public class Queue
{
//*****************************************************
// A Queue is implemented as a linked sequence of *
// QCell. A QCell comprising 2 fields: one the item *
// in the Queue (QItem); the other a link to the next *
// Queue cell. *
//*****************************************************
// QCell class only known to the Queue class itself. *
//*****************************************************
private class QCell
{
//
// QCell Fields
//
private Object QItem;
private QCell QLink;
//
// QCell Constructor
//
private QCell(Object head, QCell NextInQ)
{
QItem = head; QLink=NextInQ;
}
}
//******************************************************
// Queue Fields *
//******************************************************
// First: The QCell that contains the item at the *
// head of this Queue. *
// *
// Rest: Indicates the Queue following the first *
// Queue member. *
// Last: The most recently added Queue Item *
// Waiting: The number of items in this Queue *
//******************************************************
private QCell First;
private QCell Rest;
private QCell Last;
private int Waiting;
//******************************************************
// Queue Constructor - Initiates the Empty Queue *
//******************************************************
public Queue()
{
First = null;
Rest = null;
Last = null;
Waiting=0;
}
//******************************************************
// Queue Instance Methods *
//******************************************************
//
// Test if this Queue Is Empty
//
public boolean QIsEmpty()
{
return (Waiting==0);
};
//************************************************************
// Add a new Object to the end of this Queue; *
// The new item is added in such a way that in traversing *
// this Queue, the item will be the Last one found. Further *
// additions will be appended after this. *
//************************************************************
public void AddToQ ( Object EndofQ )
{
QCell temp;
//**********************************************************
// If this Queue is empty then the First and Last Queue *
// Cells are identical. *
//**********************************************************
if (QIsEmpty())
{
Last = new QCell(EndofQ,Last);
First = Last;
Rest = First.QLink;;
Waiting=1;
}
else
{
Last.QLink = new QCell(EndofQ,Last.QLink); // The last item is the one being added.
Last = Last.QLink;
Waiting++; // Increase Length of this Queue.
};
}
//***************************************************************
// Remove the First item (the item at the head of) this Queue *
//***************************************************************
public void TakeOffQ()
{
if (Waiting<=1) // Will leave the empty Queue
{ // after removal.
First = null; Last=null; Rest=null;
Waiting=0;
}
else
{
First = First.QLink; // Find the `new' head of the Queue.
Waiting--; // One fewer item in Queue.
if (Waiting==1) // Deal with the case that there's
{ // exactly one item left in this Queue.
Last = First;
Rest = null;
}
else
Rest = First.QLink; // If more than one; reset Rest of Queue
}; // indicator.
}
//****************************************************************
// Return the First item (the item at the head of) this Queue *
// The Queue structure is left unchanged. *
//****************************************************************
public Object GetFirstInQ()
{
if (!(Waiting==0)) // If there's anything to return
return First.QItem; // then return it.
else
return null; // otherwise return a null reference.
}
//*****************************************************************
// Return the remainder (all but the first item) of this Queue *
// The Queue structure is left unchanged. *
//*****************************************************************
public Queue GetRestOfQ()
{
Queue temporary= new Queue();
temporary.First=First; temporary.Rest=Rest;
temporary.Last=Last;
temporary.Waiting = Waiting;
temporary.TakeOffQ();
return temporary;
};
//***********************************************************
// Return a String representing the contents of this Queue *
// in a form that is suitable to print out. *
//***********************************************************
public String toString()
{
String res = new String();
Queue temporary = new Queue();
temporary.First = First;
temporary.Rest = Rest;
temporary.Last = Last;
temporary.Waiting=Waiting;
while (!temporary.QIsEmpty())
{
res = res+(temporary.GetFirstInQ()).toString()+"\n";
temporary = temporary.GetRestOfQ();
};
return res;
}
}
|
Figure 8.6: Java Realisation of Queue ADT.
At the start of this lecture it was observed that queues are a structure with which most people are familiar in everyday life. The study of the properties of queues over time is an important area in the mathematical study of Probability Theory, e.g. in considering questions such as how the length of a queue varies under different assumption about the frequency with which new arrivals occur and are served. The application we consider in this section is a very basic example of a class of systems which play an important role in advanced topic in Computer Science: Simulation Systems.
The aim of such systems is to model how a `real-world' environment would behave by using a computer program intended to `mimic' aspects of its detailed operation. There are many reasons why it is preferable to consider a computer simulation rather than a direct observation or (mathematical) analysis of a system. For example,
Construct a computer simulation program of a Supermarket Checkout, using the following modelling assumptions.
We wish to simulate this model in the following way:
In performing this simulation we wish to collect the following statistics:
Although these requirements may look rather formidable, you should note that the material that you have met so far during COMP101 and COMP102 would be more than sufficient to enable you to develop this application program unaided.
Before discussing the analysis of the problem in greater depth it is worth making a few observations about the modelling scenario:
Finally it is noted that a number of simplifications to the `real-world' situation have been assumed, e.g. we do not attempt to model: customers attempting to pay by credit card/cheque at cash-only tills; customers arriving with a month's supply of groceries at a 10-items-or-less checkout; checkout operators who cannot find the price of a particular item; customers trying to find the exact small change to pay for purchases, etc., i.e. any of the attendant irritations which anyone who uses supermarkets regularly will be only too familiar with.
We concentrate on analysing the detailed mechanics of the queue simulation, i.e.
Thus, we do not present any detailed discussion of the methods to set the parameters for the simulation environment (number of checkout tills, maximum number of customers, arrival rate etc) or those concerned with the collation and output of statistical data required. The relevant methods are fully described in the complete implementation, and their realisation can be seen to be straightforward.
As a first step the simulation can be broken down into the following stages:
The second step indicates that we want to have classes to represent:
The first of these has already been described above, however, it is useful to add one new method
that will return the current length (i.e. the value of the field Waiting) of this Queue instance.
The class diagram for the Customer Object is shown in Figure 8.7.

|
Figure 8.7: The CustomerClass Diagram.
The methods provided for a Customer instance provide access to its fields. Each customer will be associated with a unique identifying number (the client_id field), the number of rounds it will take to serve this customer (service_time), the checkout till queue that the customer joins, and, finally, the rounds on which the customer arrived at a queue and left it.
The implementation of the Customer Class is given in Figure 8.8.
//
// COMP102
// Example 13: The Customer Class to be used in
// a Supermarket simulation.
//
// Paul E. Dunne 24/11/99
//
public class Customer
{
//****************************************
// Class Fields *
//****************************************
private int client_id; // Customer number
private int service_time; // Number of purchases
private int arrival_time; // Time of arrival (in Queue)
private int departure_time; // Time of departure (from checkout area)
private int checkout_till_number;// Check out till queue assigned to.
//*******************************************************************
// The Class Methods simply instantiate and return the field values *
//*******************************************************************
public void set_id(int id)
{ client_id = id; }
//
public void set_service_time(int time)
{ service_time = time; }
//
public void set_arrived(int time)
{ arrival_time = time; }
//
public void set_depart(int time)
{ departure_time = time; }
//
public void set_checkout(int till_number)
{ checkout_till_number = till_number; }
//
public int get_id()
{ return client_id; }
//
public int get_service_time()
{ return service_time ; }
//
public int get_arrived()
{ return arrival_time ; }
//
public int get_depart()
{ return departure_time ; }
//
public int get_checkout()
{ return checkout_till_number; }
}
|
Figure 8.8: The Class to represent a Customer.
Within the main simulation system we use an array of Queue to model the checkout operation and an array of Customer to record customer information and status.
static Queue[] CheckOutQueues; // The Queue at each Checkout; static Customer[] CustomerStats; // Records Customer data. static int[] TimeLeftAtTill; // Time remaining before a till is free. |
The int array TimeLeftAtTill, is used to monitor when the customer current being served at the head of their queue is ready to leave.
We can now consider the realisation of Step 3, which forms the core of the simulation activity.
Obviously, this will comprise a while <condition> {..} structure,
//************************************************************
// Main simulation loop: Continues while customers remain *
// or the number of rounds is not completed. *
//************************************************************
while ( (!AllCustomersServed()) ||
(on_round_number < ROUNDS_TO_SIMULATE) )
{
on_round_number++; // Next simulation round;
//**********************************************
// Update the Status of each CheckOut Queue *
//**********************************************
(Step 3.1)
//*************************************************************
// Randomly decide (based on the given ARRIVAL_RATE) *
// whether a new customer has appeared. If so, then *
// initiate a new Customer record and choose a CheckOutQueue *
//*************************************************************
(Step 3.2)
//
};
|
The method AllCustomersServed, calls the QIsEmpty() instance method of the Queue associated with each Check out till. If all of these queues are empty then there are no customers remaining. Of course, this will be the situation before the simulation commences, hence the use of a minimal number of rounds (the ROUNDS_TO_SIMULATE field) in the simulation model.
In realising Step 3.1., we have to perform the following actions:
Thus,
//**********************************************
// Update the Status of each CheckOut Queue *
//**********************************************
for (int till=0; till < MAX_TILLS; till++)
{
//*****************************************************
// If current till being inspected has a non-empty Q *
// then find out the index of the Customer referenced *
// and decrease the time left until this till is free *
//*****************************************************
if (!CheckOutQueues[till].QIsEmpty())
{
firstinQ =
Integer.valueOf(CheckOutQueues[till].GetFirstInQ().toString()).intValue();
TimeLeftAtTill[till]--;
//***************************************************
// See if this customer has now been served and, if *
// so update the customer records and queue. *
//***************************************************
if (TimeLeftAtTill[till] < 1)
{
// Note the departure time.
CustomerStats[firstinQ].set_depart(on_round_number);
CheckOutQueues[till].TakeOffQ(); // Remove customer from queue.
customers_left--; // now have one less customer.
//*****************************************************
// If any customer left, serve the next in this Queue *
//*****************************************************
if (!CheckOutQueues[till].QIsEmpty())
{
nextinQ =
Integer.valueOf((CheckOutQueues[till].GetFirstInQ()).toString()).intValue();
TimeLeftAtTill[till]=CustomerStats[nextinQ].get_service_time();
};
};
};
};
|
In Step(3.2) there are 3 conditions that have to be met in order for a new Customer to be be added to the system:
Notice that in principle we could dispense with the first condition, at the expense of holding Customer records in a dynamic data structure (instead of an array). This would necessitate using a more complex mechanism in order to `look-up' specific customer information, cf the record maintenace application that we review in the next lecture.
The second condition can be interpreted as modelling the standard practice of shops not admitting new customers after closing, but continuing to deal with customers who are already being served.
For the final condition we simply obtain a random value between 0.0 and 1.0 (using the method Math.random() ), and if this value is less than the specified ARRIVAL_RATE the third condition is satisfied.
The process of adding a new customer to the system, simply involves
So we have,
//*************************************************************
// Randomly decide (based on the given ARRIVAL_RATE) *
// whether a new customer has appeared. If so, then *
// initiate a new Customer record and choose a CheckOutQueue *
//*************************************************************
if ( (Math.random() < ARRIVAL_RATE) &&
(customers_through < MAX_CUSTOMERS) &&
(on_round_number < ROUNDS_TO_SIMULATE) )
{
CustomerStats[customers_through] = new Customer();
CustomerStats[customers_through].set_arrived(on_round_number);
CustomerStats[customers_through].set_service_time(NumberofItems());
CustomerStats[customers_through].set_id(customers_through);
put_on_queue = ChooseQueueToJoin(CheckOutQueues);
//******************************************************
// If the CheckOutQueue chosen is empty, then the new *
// customer will be served at once. *
//******************************************************
if ( CheckOutQueues[put_on_queue].QIsEmpty() )
TimeLeftAtTill[put_on_queue] =
CustomerStats[customers_through].get_service_time();
CustomerStats[customers_through].set_checkout(put_on_queue);
CustomerIndex = new Integer(customers_through);
CheckOutQueues[put_on_queue].AddToQ(CustomerIndex);
customers_left++; // One more customer in the system.
customers_through++; // One more customer seen.
};
|
Figure 8.10 Adding a new customer to the system.
The complete implementation of the Check Out Simulation, including the (self-explanatory) methods for collating statistical data and obtaining simulation parameters is presented in Figure 8.11.
//
// COMP102
// Example 14: Supermarket Checkout Simulation
// Queues with random arrival and service times.
//
// Paul E. Dunne 24/11/99
//
import java.io.*;
import Customer;
import Queue;
public class CheckItAllOut
{
public static InputStreamReader input = new InputStreamReader(System.in);
public static BufferedReader keyboardInput = new BufferedReader(input);
//************************************************************
// User specified fields to be input at the simulation start *
//************************************************************
static int MAX_CUSTOMERS; // Maximum number of customers in system.
static int MAX_TILLS; // The number of checkout tills.
static int MAX_ITEMS; // The maximum number of items.
static int ROUNDS_TO_SIMULATE; // Number of simulation rounds during which
// new customers can arrive.
static double ARRIVAL_RATE; // Should be a value between 0.0 and 1.0,
// higher value == more frequent arrivals.
//***********************************************************
// The following fields allow a user to specify statistical *
// information that should be output. *
//***********************************************************
static int UPDATE_STATS=1; // Show till status every
// UPDATE_STATS iterations
static boolean FINAL_ONLY; // Only show final customer records but
// do not show statistics every iteration.
static boolean AVERAGE_MAX_ONLY; // Only show average and maximum values for
// Queue Lengths, Service Times, etc.
//************************************************************
// These fields hold various statistics that can be collated *
// as a simulation procedes. *
//************************************************************
static int customers_left=0; // The customers remaining in queues
static int customers_through=0; // The total number of customers.
static int longest_queue_length =0;
static int longest_queue;
//****************************************************
// Fields associated with the Simulation Process *
//****************************************************
static Queue[] CheckOutQueues; // The Queue at each Checkout;
static int[] TimeLeftAtTill; // Time remaining before a till is free.
static Customer[] CustomerStats; // Records Customer data.
//***************************************************
// Class Methods *
//***************************************************
//
// Input user settings for this simulation
//
public static void SetSimulationParameters() throws IOException
{
char YesNo; // To indicate statistics required.
System.out.print("How many checkout tills are there?:");
MAX_TILLS = new Integer (keyboardInput.readLine()).intValue();
System.out.println(MAX_TILLS);
System.out.print("What is the maximum number of customers?");
MAX_CUSTOMERS = new Integer (keyboardInput.readLine()).intValue();
System.out.println(MAX_CUSTOMERS);
System.out.print("What is the maximum number of items a single customer might buy?:");
MAX_ITEMS = new Integer (keyboardInput.readLine()).intValue();
System.out.println(MAX_ITEMS);
System.out.print("For how many rounds are the Check Out Queues Open?:");
ROUNDS_TO_SIMULATE = new Integer (keyboardInput.readLine()).intValue();
System.out.println(ROUNDS_TO_SIMULATE);
System.out.print("How frequently do customers arrive at checkout (0.0 < r < 1.0)?:");
ARRIVAL_RATE = new Double (keyboardInput.readLine()).doubleValue();
System.out.println(ARRIVAL_RATE);
System.out.print("How often should Checkout statistics be shown?:");
UPDATE_STATS = new Integer (keyboardInput.readLine()).intValue();
System.out.println(UPDATE_STATS);
System.out.print("Show status of each queue until completed? (y/n):");
YesNo = keyboardInput.readLine().charAt(0);
if ( (YesNo=='y') || (YesNo=='Y') )
FINAL_ONLY = false;
else
FINAL_ONLY = true;
System.out.println(YesNo);
System.out.print("Output Averages and Maxima Only? (y/n):");
YesNo = keyboardInput.readLine().charAt(0);
if ( (YesNo=='y') || (YesNo=='Y') )
AVERAGE_MAX_ONLY = true;
else
AVERAGE_MAX_ONLY = false;
System.out.println(YesNo);
System.out.println();
}
//*********************************************
// Initiate Simulation Structures *
//*********************************************
public static void StartUpQueues()
{
CheckOutQueues = new Queue[MAX_TILLS];
TimeLeftAtTill = new int[MAX_TILLS];
for (int i=0; i < MAX_TILLS; i++)
CheckOutQueues[i] = new Queue();
}
//*********************************************
// Simulation over when all Qs empty and *
// the required number of rounds is over. *
//*********************************************
public static boolean AllCustomersServed()
{
boolean ok=true;
int till_check =0;
while ((ok) && (till_check < MAX_TILLS))
{
ok = ( (ok) && (CheckOutQueues[till_check].QIsEmpty()) );
till_check++;
};
return ok;
}
//**********************************************************
// The following 4 methods output details of the customer *
// and checkout queues as the simulation procedes. *
//**********************************************************
static void ShowServedCustomer( int qnum, int cnum )
{
System.out.println("Customer at till "+qnum+" is Customer "+cnum+
" who arrived at "+ CustomerStats[cnum].get_arrived()+" and is buying "+
CustomerStats[cnum].get_service_time()+" items. "+
" Time left to wait is "+ TimeLeftAtTill[qnum]);
}
//**********************************************************
public static void OutputCheckOutStats( int after_round )
{
int firstinQ;
System.out.println("Check Out Tills after "+after_round+" rounds");
System.out.println("**********************************************");
for (int i=0; i < MAX_TILLS; i++)
{
System.out.print("Check Out Queue "+i+": ");
System.out.println(" Length: "+CheckOutQueues[i].GetWaiting() );
if (!CheckOutQueues[i].QIsEmpty())
{
firstinQ =
Integer.valueOf(CheckOutQueues[i].GetFirstInQ().toString()).intValue();
ShowServedCustomer(i,firstinQ);
};
};
System.out.println("**********************************************");
System.out.println("Customers seen: "+customers_through);
System.out.println("Customers remaining: "+customers_left);
System.out.println("**********************************************");
}
//**********************************************************
public static void OutputCustomerStats()
{
System.out.println("Customer Records after Completion");
System.out.println("**********************************************");
for (int i=0; i < customers_through; i++)
{
System.out.print("Customer "+i+": Arrived: "+
CustomerStats[i].get_arrived());
System.out.print(" Left: "+
CustomerStats[i].get_depart());
System.out.print(" Bought: "+
CustomerStats[i].get_service_time()+
" items");
System.out.println(" at till: "+
CustomerStats[i].get_checkout());
};
}
//***********************************************************************
static void OutputAverageMaxStats( int total_time )
{
int longest_wait=0;
int longest_waiting=0;
int total_waiting_time=0;
int temp_wait;
double average_wait;
System.out.println(" Average and Maxima Statistics");
System.out.println("**********************************************");
System.out.println("Total customers dealt with: "+customers_through);
System.out.println("Total time to complete serving: "+ total_time);
System.out.println("Longest queue had length "+
longest_queue_length+ " at till "+
longest_queue);
for (int i=0; i < customers_through; i++)
{
temp_wait = CustomerStats[i].get_depart()-
CustomerStats[i].get_arrived();
total_waiting_time = total_waiting_time+temp_wait;
if (temp_wait > longest_wait)
{
longest_wait = temp_wait; longest_waiting=i;
};
};
average_wait = total_waiting_time/customers_through;
System.out.println("Longest wait was "+
longest_wait+ " for customer "+
longest_waiting + " in check out queue "+
CustomerStats[longest_waiting].get_checkout());
System.out.println("Average waiting time was "+average_wait);
}
//***********************************************************************
// Select a Queue: A simple `greedy' method is used in which any new *
// customer is added to the current shortest queue *
// To compare different strategies, all that is needed is to replace *
// this method with an alternative. *
//***********************************************************************
public static int ChooseQueueToJoin ( Queue[] CheckOuts )
{
int shortest_so_far =0;
for (int i=1; i < MAX_TILLS; i++)
{
if (CheckOuts[i].GetWaiting() < CheckOuts[shortest_so_far].GetWaiting() )
shortest_so_far =i;
};
return shortest_so_far;
}
//**********************************************************************//
// The number of items bought by a new customer is randomly chosen to //
// to be a value between 1 and MAX_ITEMS. //
//**********************************************************************//
public static int NumberofItems()
{
return 1+(int) Math.rint( (MAX_ITEMS-1)*Math.random() );
}
//************************************************************//
// Main Method //
//************************************************************//
public static void main( String[] args ) throws IOException
{
int just_served; // To index CustomerStats[]
int put_on_queue; // To index CheckOutQueues[]
int on_round_number =0; // Current simulation round
int firstinQ; // Used in updating Queue/Customer
int nextinQ; //
Integer CustomerIndex; // Need Integer to store int index on Queue
//************************************************************
SetSimulationParameters(); // Get the user supplied parameters.
StartUpQueues(); // Initiate Queues, Tills
CustomerStats = new Customer[MAX_CUSTOMERS]; // And customer records.
//************************************************************
// Main simulation loop: Continues while customers remain *
// or the number of rounds is not completed. *
//************************************************************
while ( (!AllCustomersServed()) ||
(on_round_number < ROUNDS_TO_SIMULATE) )
{
on_round_number++; // Next simulation round;
//**********************************************
// Update the Status of each CheckOut Queue *
//**********************************************
for (int till=0; till < MAX_TILLS; till++)
{
//*****************************************************
// If current till being inspected has a non-empty Q *
// then find out the index of the Customer referenced *
// and decrease the time left until this till is free *
//*****************************************************
if (!CheckOutQueues[till].QIsEmpty())
{
firstinQ =
Integer.valueOf(CheckOutQueues[till].GetFirstInQ().toString()).intValue();
TimeLeftAtTill[till]--;
//***************************************************
// See if this customer has now been served and, if *
// so update the customer records and queue. *
//***************************************************
if (TimeLeftAtTill[till] < 1)
{
// Note the departure time.
CustomerStats[firstinQ].set_depart(on_round_number);
CheckOutQueues[till].TakeOffQ(); // Remove customer from queue.
customers_left--; // now have one less customer.
//*****************************************************
// If any customer left, serve the next in this Queue *
//*****************************************************
if (!CheckOutQueues[till].QIsEmpty())
{
nextinQ =
Integer.valueOf((CheckOutQueues[till].GetFirstInQ()).toString()).intValue();
TimeLeftAtTill[till]=CustomerStats[nextinQ].get_service_time();
};
};
};
};
//*************************************************************
// Randomly decide (based on the given ARRIVAL_RATE) *
// whether a new customer has appeared. If so, then *
// initiate a new Customer record and choose a CheckOutQueue *
//*************************************************************
if ( (Math.random() < ARRIVAL_RATE) &&
(customers_through < MAX_CUSTOMERS) &&
(on_round_number < ROUNDS_TO_SIMULATE) )
{
CustomerStats[customers_through] = new Customer();
CustomerStats[customers_through].set_arrived(on_round_number);
CustomerStats[customers_through].set_service_time(NumberofItems());
CustomerStats[customers_through].set_id(customers_through);
put_on_queue = ChooseQueueToJoin(CheckOutQueues);
//******************************************************
// If the CheckOutQueue chosen is empty, then the new *
// customer will be served at once. *
//******************************************************
if ( CheckOutQueues[put_on_queue].QIsEmpty() )
TimeLeftAtTill[put_on_queue] =
CustomerStats[customers_through].get_service_time();
CustomerStats[customers_through].set_checkout(put_on_queue);
CustomerIndex = new Integer(customers_through);
CheckOutQueues[put_on_queue].AddToQ(CustomerIndex);
//*******************************************************************
// Test if the queue length is greater than any seen before, and *
// update queue length statistics accordingly. *
//*******************************************************************
if (CheckOutQueues[put_on_queue].GetWaiting() > longest_queue_length)
{
longest_queue_length = CheckOutQueues[put_on_queue].GetWaiting();
longest_queue = put_on_queue;
};
customers_left++; // One more customer in the system.
customers_through++; // One more customer seen.
};
//*****************************************************************
// Output Statistics as required *
//*****************************************************************
if ( (on_round_number%UPDATE_STATS==0) &&
(!FINAL_ONLY) &&
(!AVERAGE_MAX_ONLY) )
OutputCheckOutStats(on_round_number);
};
//*************************************************************
// Simulation rounds completed, so output statistics. *
//*************************************************************
if (AVERAGE_MAX_ONLY)
OutputAverageMaxStats(on_round_number);
else
{
OutputCustomerStats();
OutputAverageMaxStats(on_round_number);
};
}
}
|
Figure 8.11: The Complete Supermarket Checkout Simulation Program.
Although this application may appear rather more substantial (in implementation terms) than those you have met previously, in fact most of the code in Figure 8.11 is concerned with methods for instantiating the simulation parameters and customising the statistical output. The core work of the actual simulation is carried out in the while loop of the main() method.