Backtracking and Searching

In a number of applications graph structures occur. The graph may be an explicit object in the problem instance as in:

Shortest Path Problem

Minimal Spanning Tree Problem

Graphs, however, may also occur implicitly as an abstract mechanism with which to analyse problems and construct algorithms for these. Among the many areas where such an approach has been used are:

Game Playing Programs

Theorem Proving Systems

Semantic Nets

Hypertext

...

Whether a graph is an explicit or implicit structure in describing a problem, it is often the case that searching the graph structure may be necessary. Thus it is required to have methods which

• Can `mark' nodes in a graph which have already been `examined'.
• Determine which node should be examined next.
• Ensure that every node in the graph can (but not necessarily will) be visited.

That is to say, (With the exception of the first node inspected)

Any new node examined must be adjacent to some node that has previously been visited.

So, search methods implicitly describe an ordering of the nodes in a given graph.

One search method that occurs frequently with implicit graphs is the technique known as

backtracking

Suppose a problem may be expressed in terms of detecting a particular class of subgraph in a graph.

Then the backtracking approach to solving such a problem would be:

Scan each node of the graph, following a specific order, until

• A subgraph constituting a solution has been found.
• or
• It is discovered that the subgraph built so far cannot be extended to be a solution.

Simple Example

Knight's Tour

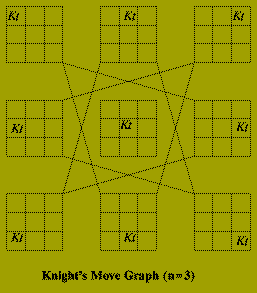
Given a natural number, n, describe how a Knight should be moved on an n times n chessboard so that it visits every square exactly once and ends on its starting square.

The implicit graph in this problem has n^2 nodes corresponding to each position the Knight must occupy. There is an edge between two of these nodes if the corresponding positions are `one move apart'. The sub-graph that defines a solution is a cycle which contains each node of the implicit graph.

Of course it is not necessary to construct this graph explicitly, in order to to solve the problem. The algorithm below, recursively searches the graph, labeling each square (i.e. node) in the order in which it is visited. In this algorithm:

• board is an n times n representation of the board; initiated to 0.
• (x,y) are the coordinates (row, column) of the current square.
• move is the number of squares visited so far.
• ok is a Boolean indicating success or failure.

type chess_board is array (1..n,1..n) of integer;
procedure knight (board : in out chess_board;
                         x,y,move : in out integer;
                         ok : in out boolean) is
w, z : integer;
begin
   if move = n^2+1 then
     ok := ( (x,y) = (1,1) );
   elsif board(x,y) /= 0 then
     ok := false;
   else
     board(x,y) := move;
     loop
       (w,z) := Next position from (x,y);
       knight(board, w, z, move+1, ok );
       exit when (ok or No moves remain);
     end loop;
     if not ok then
       board ( x,y ) :=0; -- Backtracking 
     end if;
    end if;
end knight;

Depth-First Search

Depth-first search is one method of constructing a search tree for explicit graphs.

Let G(V,E) be a connected graph. A search tree of G(V,E) is a spanning tree, T(V, F) of G(V,E) in which the nodes of T are labelled with unique values k (1 < = k < = |V|) which satisfy:

• A distinguished node called the root is labelled 1.
• If (p,q) is an edge of T then the label assigned to p is less than the label assigned to q.

Given an undirected graph G(V,E), the depth-first search method constructs a search tree using the following recursive algorithm.

procedure depth_first_search (G(V,E) : graph;
                                v : node;
                                lambda : integer;
                                T : in outsearch_tree) is
begin
   label(v) := lambda;
   lambda := lambda+1;
   for each w such that {v,w} mem E loop
     if label(w) = 0 then
       Add edge {v,w} to T;
       depth_first_search(G(V,E),w,lambda,T);
     end if;
   end loop;
end depth_fist_search;
--*******************************
-- Main Program Section
--******************************
begin
   for w mem V loop
     label( w ) := 0;
   end loop;
   lambda := 1;
   depthfirstsearch ( G(V,E), v, lambda, T);
end;

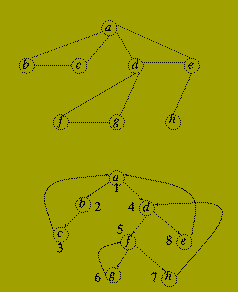
If G( V,E ) is a directed graph then it is possible that not all of the nodes of the graph are reachable from a single root node. To deal with this the algorithm is modified by changing the `Main Program Section' to

begin
  for each w in V loop
    label( w ) := 0;
  end loop;
  lambda := 1;
  for each v mem V loop
    if label( v ) = 0 then
      depthfirstsearch ( G(V,E),v,lambda,T );
    end if;
  end loop;
end;

The running time of both algorithms, input G( V,E ) is O( |E| ) since each edge of the graph is examined only once.

It may be noted that the recursive form given, is a rather inefficient method of implementing depth first search for explicit graphs.

Iterative versions exist, e.g. the method of Hopcroft and Tarjan which is based on a 19th century algorithm discovered by Tremaux. Depth-first search has a large number of applications in solving other graph based problems, for example:

Topological Sorting

Planarity Testing

One disadvantage of depth first search as a mechanism for searching implicit graph structures, is that expanding some paths may result in the search process never terminating because no solution can be reached from these. For example this is a possible difficulty that arises when scanning proof trees in Prolog implementations.

Breadth-first Search is another search method that is less likely to exhibit such behaviour.

lambda := 1; -- First label
CurrentLevel := {v}; -- Root node
while CurrentLevel /= (es loop
  for each v mem CurrentLevel loop
    NextLevel := Nextlevel union 
                 Unmarked neighbours of v;
    if label( v ) = 0 then
      label( v ) := lambda;
      lambda := lambda + 1;
    end if;
  end loop;
  CurrentLevel := NextLevel;
  NextLevel := (es;
end loop;

Thus each vertex labelled on the k'th iteration of the outer loop is `expanded' before any vertex found later.

• Overview
• Introduction
• Divide-and-Conquer Algorithms
• Dynamic Programming Algorithms
• The Greedy Method

PED Home Page