


Next: Procedure
Up: Problem and Procedure
Previous: Problem and Procedure
We assume that the language
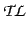 of the first-order temporal logic
is constructed in the standard way (see i.e.
[HWZ00])
from a classical (non-temporal) first-order language
of the first-order temporal logic
is constructed in the standard way (see i.e.
[HWZ00])
from a classical (non-temporal) first-order language 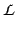 and
a set of future-time temporal
operators `
and
a set of future-time temporal
operators `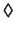 '
(sometime), `
'
(sometime), `
 ' (always), and `
' (always), and `
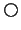 ' (in the next
moment).
Here,
' (in the next
moment).
Here, 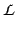 does not contain equality or functional symbols.
Formulae of
does not contain equality or functional symbols.
Formulae of
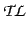 are interpreted in first-order temporal structures
with constant domain. We assume the rigid semantics for the variables and
constants. We assume also the standard notions of
satisfiable and valid formulae (evaluated in initial worlds of
temporal structures).
A first-order temporal
specification is a triple
are interpreted in first-order temporal structures
with constant domain. We assume the rigid semantics for the variables and
constants. We assume also the standard notions of
satisfiable and valid formulae (evaluated in initial worlds of
temporal structures).
A first-order temporal
specification is a triple
 where
where 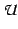 and
and 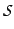 are
the universal part and the initial part, respectively,
given by finite sets (conjunctions) of (nontemporal) first-order formulae, and
are
the universal part and the initial part, respectively,
given by finite sets (conjunctions) of (nontemporal) first-order formulae, and 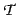 is
the temporal part given by a finite set (conjunction) of temporal step
formulae.
A temporal step formula has the following form:
is
the temporal part given by a finite set (conjunction) of temporal step
formulae.
A temporal step formula has the following form:
where 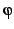 and
and 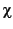 are first-order formulae with the (possibly empty)
sequence of free variables
are first-order formulae with the (possibly empty)
sequence of free variables 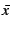 .
A temporal specification
.
A temporal specification
 is just a syntactical form of
representation of the temporal formula
is just a syntactical form of
representation of the temporal formula
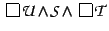 .
If any temporal step formula of the specification
.
If any temporal step formula of the specification 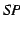 has one of the
following forms:
has one of the
following forms:
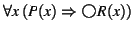 , or
, or
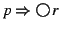 , where
, where 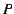 and
and 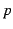 are unary (i.e. one-place) predicate symbol and propositional
symbol, respectively,
are unary (i.e. one-place) predicate symbol and propositional
symbol, respectively, 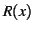 and
and 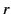 are boolean expressions composed
from one-place predicates and propositional symbols, respectively, then
the specification is called monodic
[HWZ00,BDFL02].
Given a first-order temporal specification
are boolean expressions composed
from one-place predicates and propositional symbols, respectively, then
the specification is called monodic
[HWZ00,BDFL02].
Given a first-order temporal specification 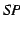 and a ground first-order
formula
and a ground first-order
formula 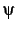 ,
a ground induction problem is that where the validity of
the formula
,
a ground induction problem is that where the validity of
the formula
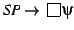 must be established
must be established



Next: Procedure
Up: Problem and Procedure
Previous: Problem and Procedure
Alexei Lisitsa
2003-06-13