


Next: Implementation
Up: Problem and Procedure
Previous: Temporal specifications and ground
In the paper [BDFL02] a method for solving the ground induction problem
was proposed and its completeness for the case of monodic specifications was
established. We decsribe here a procedure, implementing this method,
applicable to all the temporal specifications defined above.
The problem.
Given: A temporal specification
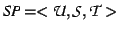
with
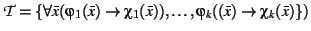 and a first-order formula
and a first-order formula 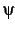 Decide: Is
Decide: Is
 valid ?
valid ?
The procedure.
Stage 1. Saturation of the universal part
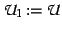 ;
;
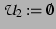 ;
;
while
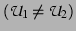 do
do
{
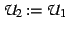 ;
;
for all subsets
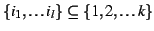
do
{
if
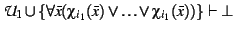
then
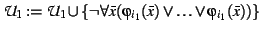 ;
;
if
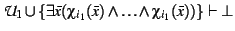
then
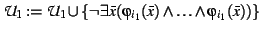 ;
;
}
}
Stage 2. Checking the start conditions
if
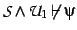 then STOP with answer ``No'' ;
then STOP with answer ``No'' ;
else Continue;
Stage 3. Generation of merged rules
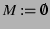
for all subsets
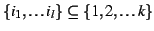
do
{
if (
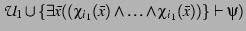
then
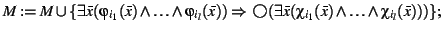
if (
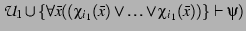
then
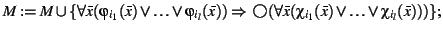
}
Stage 4. Checking the loop conditions
for all subsets
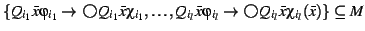 (
(
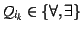 )
)
do
{
if
 and
and
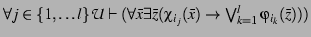
then STOP with answer ``Yes''
}
STOP with answer ``I don't know''.
The procedure is correct in the following sense: if it stops and produces
the answer "Yes" then, indeed,
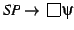 is valid (by
straightforward check, see [BDFL02]).
However,
in general it is incomplete and may produce an ``I don't know'' answer for a valid
formula. In the case of monodic specifications it is complete modulo first-order
derivability, i.e. if one assumes the existense of oracle resolving the tasks
of the kind
is valid (by
straightforward check, see [BDFL02]).
However,
in general it is incomplete and may produce an ``I don't know'' answer for a valid
formula. In the case of monodic specifications it is complete modulo first-order
derivability, i.e. if one assumes the existense of oracle resolving the tasks
of the kind
 for the first-order formulae
for the first-order formulae
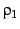 and
and 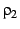 .
To obtain the complete procedure in the case of real semi-decision
(proof search) procedures for first-order logic,
one needs to apply special strategies, ensuring the (uniform) progress in the
proof search for all first-order formulae generated.
.
To obtain the complete procedure in the case of real semi-decision
(proof search) procedures for first-order logic,
one needs to apply special strategies, ensuring the (uniform) progress in the
proof search for all first-order formulae generated.



Next: Implementation
Up: Problem and Procedure
Previous: Temporal specifications and ground
Alexei Lisitsa
2003-06-13