


Next: Bibliography
Up: Invariant Serach via Temporal
Previous: Procedure
The method described above has been implemented as a part of a
prototype prover for temporal specifications in the 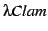 envinronment [RSG98].
envinronment [RSG98]. 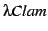 is a proof
planning [Bun88] system, implemented in the Teyjus
implementation of
is a proof
planning [Bun88] system, implemented in the Teyjus
implementation of 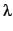 Prolog [Tey,Lpro],
a higher-order typed logic programming language A proof plan is a representation of a proof at some level of abstraction
(usually above the level of basic inference rules, but not necessarily so).
In
Prolog [Tey,Lpro],
a higher-order typed logic programming language A proof plan is a representation of a proof at some level of abstraction
(usually above the level of basic inference rules, but not necessarily so).
In 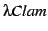 a proof plan is generated from a goal by the application of
planning operators called proof methods.
Atomic methods are suitable for the implementation of basic proof
rules, or automated proof procedures, while compound methods are used to build
more complex proof strategies (or heuristics) from atomic methods.
The features of the system are as follows:
a proof plan is generated from a goal by the application of
planning operators called proof methods.
Atomic methods are suitable for the implementation of basic proof
rules, or automated proof procedures, while compound methods are used to build
more complex proof strategies (or heuristics) from atomic methods.
The features of the system are as follows:
- Our system works with arithmetical translations of temporal formulae, i.e.
with translation into two-sorted first-order formulae, with one sort being
the natural numbers. This is done for better integration with a body of proof
plans and methods already existing in
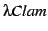 for arithmetic.
for arithmetic.
- For first-order (non-temporal) proving called within the
prover an atomic method proof_tableau re-implementing
the simple, but convenient LeanTap tableaux prover [BP95]
in
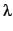 Prolog, is used. Higher-order unification and
Prolog, is used. Higher-order unification and 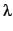 -terms as
the data structure
in
-terms as
the data structure
in
 allows us to re-implement LeanTap in more direct and
declarative way, without using the "non-logical" copy_term predicate and with
allows us to re-implement LeanTap in more direct and
declarative way, without using the "non-logical" copy_term predicate and with
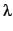 -terms presenting the quantifier's bindings.
Efficiency of such
-terms presenting the quantifier's bindings.
Efficiency of such 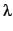 LeanTap
proves to be comparable with the original LeanTap,
running on Sicstus Prolog [Lis03].
LeanTap
proves to be comparable with the original LeanTap,
running on Sicstus Prolog [Lis03].
- We have inplemented, so far, the simplest strategy concerning the depth of
search within first-order tableau prover - it is invoked with the
pre-defined constant depth bound.
We consider the possibility to use the proof planning
methodology to control the depth of search. Simple heuristics based on the
number of quantifiers (or quantifier depth) may be used here.
- The kernel of the system is an atomic method called
mutual_induction, implementing the above procedure.
It uses the higher-order unification of
 to
separate a given a set of formulae into the sets
of step rules and the universal and start parts, and
also to produce subformulae, which are used later to construct the goals for
first-order theorem proving (conditions to check in the Stages 1-4.)
After that,
mutual_induction invokes four sub-methods (
to
separate a given a set of formulae into the sets
of step rules and the universal and start parts, and
also to produce subformulae, which are used later to construct the goals for
first-order theorem proving (conditions to check in the Stages 1-4.)
After that,
mutual_induction invokes four sub-methods (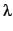 -Prolog
predicates) implementing the Stages 1-4 of the procedure.
-Prolog
predicates) implementing the Stages 1-4 of the procedure.
- The sets of formulae are presented as Prolog lists and a simple procedure for
generating all its subsets is used. Simple
optimization, based on the fact that any superset of an inconsistent set of
formulae is itself inconsistent, is applied at Stage 1.
It remains to be explored whether the use of higher-order features
of
 may optimize the search for minimal inconsistent subsets.
may optimize the search for minimal inconsistent subsets.
Initial experiments have indicated the viability of our approach. The system
is able to prove all the examples of temporal specifications
given in [BDFL02].
Our further work is to develop and implement
optimizations for the proof search procedure together with imporved
strategies/heuristics.



Next: Bibliography
Up: Invariant Serach via Temporal
Previous: Procedure
Alexei Lisitsa
2003-06-13