|
|
|
First example includes a static array of instances, and the second a dynamic array of instances of the Point_2D defined previously (and which in turn creates and uses an instance of the class Triangle).
1. INTRODUCTION |
The elements in an array do not have to be made up of primitive types, they can be compound types. For example the elements of an array may be other arrays or instances of a particular class. Here we will discuss arrays of instances (arrays of arrays are not part of the COMP101 syllabus).
A SIMPLE EXAMPLE |
|
In an earlier example program fragment we presented a class Dec2Hex, which had one field, the constant MAX_NUM_DIGITS which was set to 3; and three methods associated with it (Figure 1) used to output numbers in hexadecimal format. 
Figure 1: Class diagram for Dec2Hex class Suppose we now wish to create an array of instances of the class (type) Dec2Hex. We could do this as follows: Dec2Hex [] hexArray = new Dec2Hex[LENGTH] Here we have declared an array of N elements (N = LENGTH) where each element is an instance of the class Dec2Hex. To initialize this array we must use a constructor thus:
for (index=LOWER_BOUND;index < LENGTH;
index++)
hexArray[index] = new
Dec2Hex( < SOME_VALUE > );
Note that this requires some modification of the Dec2Hex class so that it includes:
|
Any changes we make to the Dec2Hex class should be such that any application program that we might have written previously, using the class as was, still operates as expected. The previous version of the Dec2Hex class operated using the default constructior:
public Dec2Hex() {
}
If we write our own constructor this will over-ride the default constructor thus, to ensure that any previous application program continues to operate, we must also include a default constructor of the above form in our revised Dec2Hex class. The required modifications to the Dec2Hec class are presented in Table 1. A revised class diagram for the Dec2Hex class is given in Figure 2. 
Figure 2: Class diagram showing revisions to Dec2Hex class The application Class (Dec2HexAppVer2) presented in Table 2 uses the above constructs to create an array of 256 instances of the class Hex2dex, instantiates the value attribute for each of these elements, converts each value to hex' format, and then outputs the entire array. The output is shown in Table 3. |
// DECIMAL TO HEXADECIMAL COMVERSION
// Frans Coenen
// Thursday 1 July 1999
// Revissions Wednesday 23 November 2002
// The University of Liverpool, UK
class Dec2Hex {
// ------------------ FIELDS ------------------------
private int value;
private static final int MAX_NUM_DIGITS = 3;
// ------------------ METHODS ------------------------
public Dec2Hex() {
}
public Dec2Hex(int number) {
value = number;
}
/* ------ OUTPUT HEXADECIMAL NUMBER ------ */
/* Output a hexadecimal number with leading zeroes. */
public void convertDec2Hex(int count) {
final int HEX_BASE = 16;
// Base case
if (value < HEX_BASE) {
padWithZeros(count);
outputHexDigit(value);
}
// Recursive step
else {
convertDec2Hex(value/HEX_BASE,count=count+1);
outputHexDigit(value%HEX_BASE);
}
}
public void convertDec2Hex(int number, int count) {
final int HEX_BASE = 16;
// Base case
if (number < HEX_BASE) {
padWithZeros(count);
outputHexDigit(number);
}
// Recursive step
else {
convertDec2Hex(number/HEX_BASE,count=count+1);
outputHexDigit(number%HEX_BASE);
}
}
< REST OF CODE SAME AS BEFORE >
|
Table 1: Modified Dec2Hex class
// DECIMAL TO HEXADECIMAL VERSION 2 APPLICATION 2
// Frans Coenen
// Thursday 12 July 1999
// The University of Liverpool, UK
class Dec2HexAppVer2 {
// ------------------ FIELDS ------------------------
static private final int LOWER_BOUND = 0;
static private final int LENGTH = 256;
static private final int NUMBERS_PER_LINE = 15;
static private Dec2Hex [] hexArray = new Dec2Hex[LENGTH];
// ------------------ METHODS ------------------------
/* Main */
public static void main(String[] args) {
int index;
int newLineCounter=0;
// Initialise Dec2Hex array of given size.
hexArray = new Dec2Hex[LENGTH];
for (index=LOWER_BOUND;index < LENGTH;index++)
hexArray[index] = new Dec2Hex(index);
// Output
for(index=LOWER_BOUND;index < LENGTH;index++) {
hexArray[index].convertDec2Hex(0);
System.out.print(" ");
if (newLineCounter == NUMBERS_PER_LINE) {
System.out.print("\n");
newLineCounter=0;
}
else newLineCounter++;
}
// End
System.out.println("\n");
}
}
|
Table 2: Array of (Dec2Hex) objects example application class
0000 0001 0002 0003 0004 0005 0006 0007 0008 0009 000A 000B 000C 000D 000E 000F 0010 0011 0012 0013 0014 0015 0016 0017 0018 0019 001A 001B 001C 001D 001E 001F 0020 0021 0022 0023 0024 0025 0026 0027 0028 0029 002A 002B 002C 002D 002E 002F 0030 0031 0032 0033 0034 0035 0036 0037 0038 0039 003A 003B 003C 003D 003E 003F 0040 0041 0042 0043 0044 0045 0046 0047 0048 0049 004A 004B 004C 004D 004E 004F 0050 0051 0052 0053 0054 0055 0056 0057 0058 0059 005A 005B 005C 005D 005E 005F 0060 0061 0062 0063 0064 0065 0066 0067 0068 0069 006A 006B 006C 006D 006E 006F 0070 0071 0072 0073 0074 0075 0076 0077 0078 0079 007A 007B 007C 007D 007E 007F 0080 0081 0082 0083 0084 0085 0086 0087 0088 0089 008A 008B 008C 008D 008E 008F 0090 0091 0092 0093 0094 0095 0096 0097 0098 0099 009A 009B 009C 009D 009E 009F 00A0 00A1 00A2 00A3 00A4 00A5 00A6 00A7 00A8 00A9 00AA 00AB 00AC 00AD 00AE 00AF 00B0 00B1 00B2 00B3 00B4 00B5 00B6 00B7 00B8 00B9 00BA 00BB 00BC 00BD 00BE 00BF 00C0 00C1 00C2 00C3 00C4 00C5 00C6 00C7 00C8 00C9 00CA 00CB 00CC 00CD 00CE 00CF 00D0 00D1 00D2 00D3 00D4 00D5 00D6 00D7 00D8 00D9 00DA 00DB 00DC 00DD 00DE 00DF 00E0 00E1 00E2 00E3 00E4 00E5 00E6 00E7 00E8 00E9 00EA 00EB 00EC 00ED 00EE 00EF 00F0 00F1 00F2 00F3 00F4 00F5 00F6 00F7 00F8 00F9 00FA 00FB 00FC 00FD 00FE 00FF |
Table 3: Output from application program given in Table 2
3. EXAMPLE PROBLEM - VOYAGE DISTANCE3.1. Requirements
A set of Nassi-Shneiderman diagrams for the VoyageDistance class is given in Figure 5. 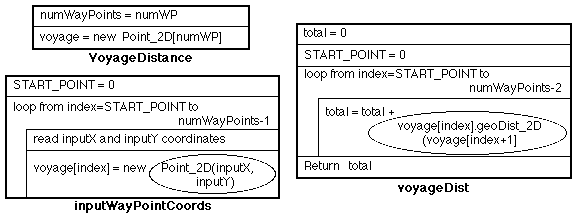
Figure 5: Nassi-Shneiderman charts for voyage distance class. 3.3.2 VoyageDistApp Class
A series of Nassi Shneiderman charts describing the above methods are given in Figure 6. 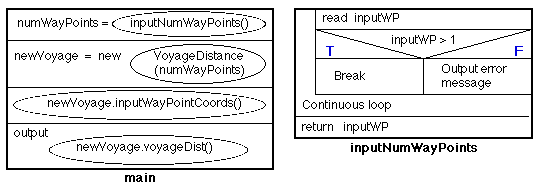
Figure 6: Nassi-Shneiderman charts for voyage distance application class. 3.4. ImplementationThe implementation for the above is given in Tables 4 and 5.
Table 4: Voyage distance class implementations
Table 5: Voyage distance application class implementation 3.5. Testing
Created and maintained by Frans Coenen. Last updated 10 February 2015 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||