Aims and Objectives: Provide an opportunity for students to apply their knowledge of pre-test loop constructs ("for" and "while") taught in week 7, and to buid a simple class hierarchy.

1. REQUIREMENTS

Over the centuries many mathematicians have proposed progressions for estimating PI. Including:

(1) Francois Vieta (1540-1603), a French mathematician who proposed the sequence:

 2     sqrt(2)   sqrt(2+sqrt(2))   sqrt(2+sqrt(2+sqrt(2)))   sqrt(2+sqrt(2+sqrt(2+sqrt(2))))
---- = ------- x --------------- x ----------------------- x ------------------------------- x ....
 PI       2                2                     2                           2

Considering only the first four terms:

  2      1.41421     1.84776     1.96157     1.99037 
---- = --------- x --------- x --------- x --------- 
 PI         2           2           2           2

     = 0.70710 x 0.92388 x 0.98078 x 0.99518 = 0.63764 

Which means that:

PI = 2/0.63764 = 3.13655

Note that in Vieta's progression, for each term, we add 2 to the dividend of the previous term and then find the square root. After only a few terms this gives a good approximation, for example 20 terms gives the estimate 3.1415926535886185, which is very close to the estimation we use today (3.141592653589793).

(2) John Wallis (1616-1703), an English Mathematician , who proposed:

 PI     2     2     4     4     6     6     8     8     10     10
---- = --- x --- x --- x --- x --- x --- x --- x --- x ---- x ---- x ....
 2      1     3     3     5     5     7     7     9      9     11

Considering only the first eight terms:

 
     = 2.0 x 0.66667 x 1.33333 x 0.8 X 1.2 x 0.85714 x 1.14286 x 0.88888 
     
     = 1.48608  

Which means that:

PI = 2 x 1.48608 = 2.97215 

Note that for Wallis's progrtession the dividend and divisor are alternatively incremented by 2. Wallis's progression does not operate as efficiently as that proposed by Franciscus Vieta, however if we multiply the first 20,000 terms we get 3.1415141186819087!

Francois Vieta (1540-1603) 1

John Wallis (1616-1703) 2

[1] Design, implement and test a class hierarchy of the form shown in Figure 1, which has a super-class PIestimation and two sub-classes (Vieta and Wallis), which can be used to produce estimates of PI, using either the method proposed by Franciscus Vieta or that of John Wallis. You should allow for a "number of terms" value to be supplied by the user. [2] Then design and implement an application class that uses the classes in the hierarchy to produce estimates for PI using the two approaches outlined above.

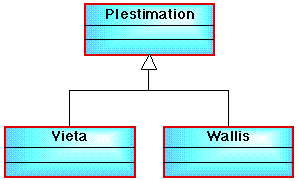
Figure 1: Incomplete class diagram for PI estimation practical

Test the programs using appropriate testing techniques including loop testing.

HINTS:

Point of interest: Knowing PI to 39 decimal places is sufficient to calculate the circumference of the universe accurate to the radius of a hydrogen atom, however this has not prevented computer scientists from calculating PI to as many decimal places as possible (Singh 1997). In 1996 Yasumasa Kanada of the University of Tokyo calculated PI to six billion decimal places. Singh also reports that the Chudnovsky brothers in New Tork are aiming to reach a trilion decimal places!

2. REPORT

Your solution should comprise the following:

1. A report in the form of a single Microsoft Word file.
2. The Java source files of your implementations for both Parts [1] and [2].

The report should comprise the following sections:

1. A summary of the requirements statement (Section 1 above).
2. For Part [1]
   • Analysis: Your analysis of the problem comprising: (i) a Class Diagram outlining the proposed class structure/hierarchy, and (ii) a set of summary tables describing the fields, constructors and methods for each class you intend to create.
   • Design: Detailed designs for the methods you intend to include, described using Nassi-Shneiderman charts, and a high-level Activity Diagram describing the "paths" through your code.
3. For Part [2]
   • Analysis: A Class Diagram of your proposed "application class" supported by summary tables.
   • Design: Detailed designs for the methods you intend to include in your application class comprising Nassi-Shneiderman charts and activity diagrams.
4. Testing: A set of test cases to test the code developed in parts [1] and [2] together with the output from your program as a result of running these test cases (in particular the loops will require appropriate testing).

Rember that all supporting documentation (i.e. excluding your source files) should be prepared as a single Microsoft Word file.

3. SUBMISSION

Once completed you should "up load" your Java source files (extension .java) and your word document to the CS department's electronic "practical assignment submission" system.

4. MARK SCHEME

Marks will be awarded for:

1. Analysis and design (30%)
2. Implementation (30%)
3. Testing (30%)
4. Write Up (10%)

With the total number of available marks distributed as indicated

Remember:

1. Guidance notes for the execution of COMP101 practicals.
2. General guidance notes on COMP101 practicals and course work with respect to: the presentation of work, the COMP101 marking scheme and University's late submission policy.
3. It is better to hand in an incomplete piece of work rather than nothing at all as this will result in some marks being awarded, while the latter option is guaranteed to result in a mark of 0!
4. Although the exchange of ideas between students is encouraged, student collaboration should not extend to the submitting of identical, or near identical, pieces of work.

2. REFERENCES

1. Arndt Brünner (2002). Biographisches zu einigen bedeutenden Mathematikern. http://home.t-online.de/home/arndt.bruenner/mathe/Allgemein/bios.htm. No longer availabel!
2. Lindy Web (2002). Mathmaticians. http://lhs.lindy.k12.ny.us/hs/Math%20Web%20Site/Famous%20Mathematicians/Mathematicians.htm. No longer availabel!
3. Singh, S. (1997). Fermat's Last Theorem. Fourth Estate, London.

Created and maintained by Frans Coenen. Last updated 30 October 2006